Randall D. Peters
Department of Physics
Mercer University

Wednesday, Jan 19, 2005, 4:30pm
Willet Science Center 101

Some Mathematical Foundations
 of Deterministic Chaos in Physics

To the uninitiated there appears to be a great divide between the way mathematicians and physicists study the ‘new science’ of chaos.  A primary difference between their modeling methods can be shown to result from the choice of size for a time-step.  Physicists generally prefer to describe a system in terms of state variables (such as position and velocity) which vary continuously with the time t; whereas mathematicians prefer to work with ‘maps.’  As will be shown in this seminar, the connection between these two representations can be greatly clarified by applying the methods of Hamiltonian mechanics when generating the differential equations of motion.  The motion thus prescribed is naturally approximated (for computer analysis) by means of coupled, lower-order finite-difference equations involving δt.  These can be used to either (i) generate graphs to show the evolutionary character of the system as preferred by physicists, through working with a small δt (to produce time-plots, or phase-space plots, or Poincare’ sections); or to (ii) produce an associated map that is preferred by mathematicians, by setting δt = 1.  Some examples will be given, including the Chirikov (or standard) map that is intimately related to the chaotic pendulum.  (A 1993 photograph of plasma physicist Chirikov will be shown, taken in Russia by Peters while visiting Novosibirsk, Siberia)  A two dimensional map discovered by Peters, through the study of a torsion-gravity pendulum (http://physics.mercer.edu/petepag/pend.htm), will be discussed.  Depending on the size of a single parameter, this map is able to express features of three different and important physical systems: (i) the harmonic oscillator, (ii) the Duffing oscillator, and (iii) the chaotic pendulum. 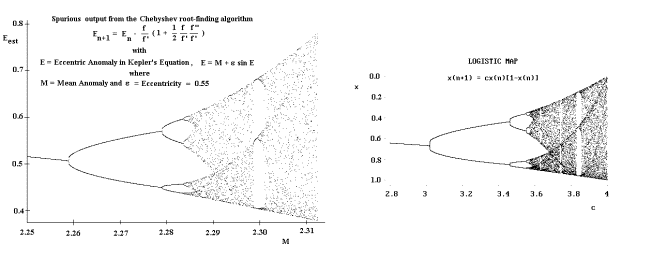Best known through the one-dimensional map known as the logistic equation, the period doubling route to chaos will be discussed in terms of the fundamental constant discovered by physicist Mitchell Feigenbaum.  The practical importance of the Feigenbaum constant δ=4.699s… (c.f., http://mathworld.wolfram.com/FeigenbaumConstant.html) is still largely unknown.   One hint of its importance will be shown where an attempt to solve Kepler’s equation by means of an ‘improved Newton’ (Chebyshev) method met with spurious results analogous to the period-doubling route to chaos in the logistic equation.