Jose L. Balduz Jr.
Department of Physics
Mercer University

Wednesday, 1/26/2005, 4:30 pm
Willet Science Center 101

The Graph Laplacian as a Tool
 for Network Resistance
 and Discrete Space Distance

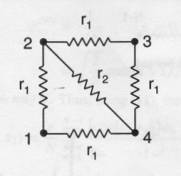
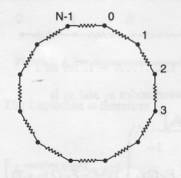
The Laplacian of a graph is useful in a variety of contexts in and outside of physics, especially when one has the solutions to the associated eigenproblem. This is illustrated in a recent paper by F. Y. Wu,

 “Theory of resistor networks: the two-point resistance,”
 J. Phys A: Math. Gen. 37 (2004) 6653-6673.

In this paper Wu constructs a Laplacian matrix from the individual resistor values in a network, then uses its eigenvalues and eigenvectors to find the effective electrical resistance from one point to another. We will make a simple analogy to transfer the paper’s main result to the physically distinct problem of defining a proper distance between points in a graph of discrete space; this is shown to satisfy the triangle inequality. Finally we will compare these results to those of a dynamical method presented in a previous talk (10/13/2004, “Modeling Space with Simple Graphs”).