Soup-can Pendulum
Copyright 2000 by Randall D. Peters
Department of Physics
1400 Coleman Ave.
Mercer University
Macon, Georgia 31207
Abstract
In these studies, a vegetable can containing fluid was swung as a pendulum
by supporting its end-lips with a pair of knife edges. The motion was measured
with a capacitive sensor and the logarithmic decrement in free decay was
estimated from computer collected records. Measurements performed with nine
different homogeneous liquids, distributed through six decades in the viscosity
h, showed that the damping of the system is dominated
by h rather than external forces from air or the
knife edges. The log decrement was found to be maximum (0.28) in the vicinity
of h = 0.7 Pa·s and fell off more than 15 fold
(below 2 ×10-2) for both small viscosity
(h <
1×10-3 Pa·s) and also for large viscosity
(h > 1
×103 Pa·s). A simple model has been formulated, which
yields reasonable agreement between theory and experiment by approximating
the relative rotation of can and liquid.
1 Introduction
Pendulum damping is usually thought of as originating from forces external
to the oscillating member-as for example, from air or knife edges. There
are many mechanical oscillators, however, for which the primary damping mechanism
is internal friction. A recently studied example is that of the long-period
pendulum [1]. The present paper describes another
pendulum, whose period is short ( <
0.5 s), and which is also influenced primarily by internal
friction. The study was partly motivated by the mechanics of rolling vegetable
cans. Although a proper interpretation of some results can be
tricky[2], it has become commonplace for physics
teachers and their students to compare the rolling speed of two different
vegetables on an inclined plane. The popularity of these demonstrations suggested
that it might also be fascinating to study a ``pendulating" vegetable can.
Part of the fascination with the soup-can pendulum derives from early
observations in which behavior differences of the type illustrated in Fig.
1 were noted.
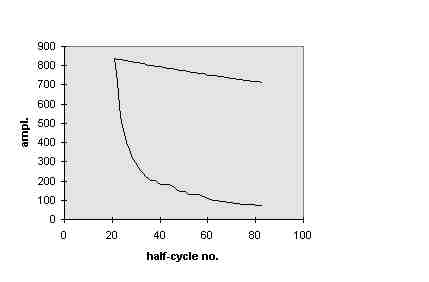
Figure 1. Comparison of the decay of two different vegetable cans.
Shown in this figure is the decay in peak-to-peak amplitude of the motion
for each of two different vegetables: (i) blackeyed peas, and (ii) sweet
peas. Unlike the blackeyed peas case, for which there is little damping,
a dramatic loss occurs when the pendulum is a can of sweet peas. The vertical
axis of this graph is peak-to- peak amplitude of the pendulum motion based
on analog to digital counts (described later), and it is plotted versus time
expressed in half-cycle integers. In all studies presently reported, the
period of oscillation is in the vicinity of 0.45 s, using common vegetable
cans of size 7.4 cm dia. by 11.2 cm length, and 56 g empty can mass. Although
some variations in period were noted from case to case, as expected; these
changes were small compared to the primary variation, which is the damping.
Later studies are planned in which the second order effects of period will
be addressed. The remarkable difference between the sweet peas and blackeyed
peas was not anticipated by means of other comparisons. For example, shaking
the cans revealed a significant volume of water packed with each of the
vegetables. In a rolling comparison it was found that the sweet peas were
faster than the blackeyed peas down an incline, but not with a huge difference
as in Fig. 1. Another interesting feature of Fig. 1 are the ``steps" in the
decay of the sweet peas. Apparently the peas tend to organize in groups,
the size of which depends on pendulum amplitude. Thus there is evidence for
granularity giving rise to self-organized
criticality[3]. The understanding of these
effects must also await future studies.
2 Pendulum Design
Shown in Fig. 2 are (i) the support structure for the pendulating can and
(ii) the placement of the symmetric differential capacitive (SDC) sensor
to monitor position.
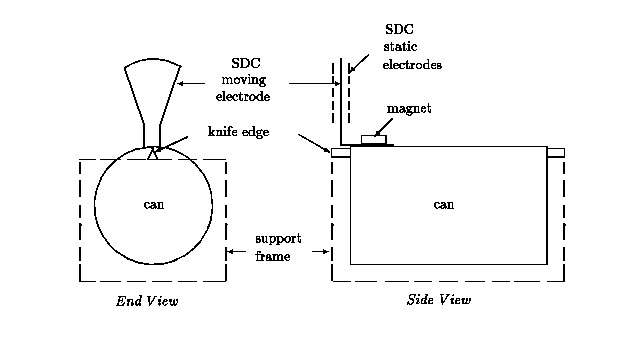
Figure 2. Illustration of the soup-can pendulum.
The fixed electrodes of the sensor were attached to the support frame with
super glue, near the top end of the can, using two pieces of 8 mm thick lucite.
The frame was constructed from a 11 cm long section of ``c" channel aluminum
of 8 mm wall thickness and 15.3 cm width. Two small aluminum pieces to hold
the knife edges were welded to the 4 cm high sides, using a tungsten inert
gas, or TIG welder. These optionally could have been attached with screws.
The clearance between the bottom of a can and the frame is
» 1 cm. The knife edges were made from
a section of bandsaw blade 0.5 mm thickness, 1.2 cm width. The teeth were
ground off the blade, and each knife edge was sharpened in the vicinity of
the end which contacts the lip of the can. One of these was press fitted
into a slot cut in its small aluminum holder, and the other was hinged with
a small steel pin so that the can may be easily mounted and dismounted from
the frame. The doubly differential capacitive sensor, which is described
elsewhere [4] comprises two sets of stationary
electrodes held in parallel proximity, and a third planar electrode which
moves between the stationary pair. For the present experiments, the moving
electrode was cut with scissors from thin sheet aluminum. A near right angle
bend in the lower section of this ``fan-shaped" piece permits it to be fixed
in position on top of the can by a small magnet.
3 Experimental Technique
When filled with inhomogeneous vegetables, the motion of the can pendulum
is hopelessly complicated, relative to a first effort at theoretical modelling
of the system. The difficulty of such a task may be appreciated by simply
inspecting the sweet pea decay case of Fig. 1. For this reason we chose to
first look at decays (for serious study) in which the can is filled with
a variety of different homogeneous liquids, whose primary difference is their
viscosity, h. In the results which follow, it will
be seen that a range in h of more than six orders
of magnitude is readily achieved, using only liquids which are common to
most physics departments. To insure a meaningful comparison among runs with
different liquids, the vegetable can selected for use was in all cases the
one whose dimensions were indicated in the discussion of Fig. 1. Following
the purchase of a can from the grocery store, the vegetable contents had
to be emptied. To facilitate mechanical integrity after refilling, the lid
was separated from the body of the can using a can-opener (Culinare) that
cuts through the narrow outside crimp in the end-lip. Not only does this
technique result in safe products of separation, since there are no sharp
edges on either the can or its lid; but also their smooth separation permits
the pair to be rejoined, after filling with a test liquid, by means of a
thin layer of glue.
3.1 Data Collection
The analog data from the sensor electronics is input to the 33 MHz 486 PC
computer by means of a Metrabyte 1401 analog to digital (A/D) converter.
Software of both acquisition and processing types was written in QuickBasic
(compiled), and the hybrid code had in some cases been written by Metrabyte
and in other cases by the author. Two different modes of operation are employed.
The setup mode is a real-time one in which the duration of the record graphed
on the monitor, and the full-scale sensitivity of the electronics, are chosen
after a prompt is displayed. This permits the operator to adjust the electronics
offset for a mean output that is in the vicinity of zero. The pendulum
displacement is mapped vs time on the monitor using the 'pset' software command.
In this mode, the computer emulates an old-fashioned strip-chart recorder.
The second mode is one in which a record of 2048 points (2 K) is written
to memory of the computer for later analysis. During collection of the record,
no graphical information is available for viewing. For all cases presently
reported, the 2 K records from which figures were produced, were collected
using a full scale sensitivity of (+/-) 0.1 V. For the sensor used in
these experiments, the calibration constant corresponding to this A/D
sensitivity, was 1.5 ×105 counts/rad for counts in the range
-4095 to 4096.
It is possible to view the raw data directly, as illustrated in Fig. 3, which
shows the vast difference between a can filled with glycerin and a reference
case for which there is insignificant internal friction.
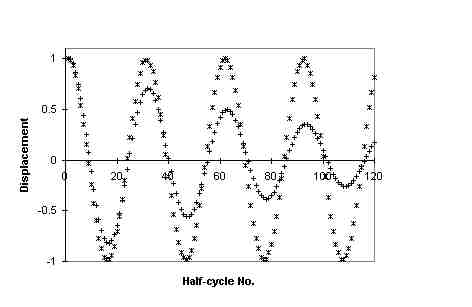
Figure 3 Decay of glycerin compared to a reference decay.
For this comparison, the ordinate values were normalized to the initial peak
amplitude, which is a straightforward operation with the Microsoft Excel
software that was used to produce all graphs. For a given case, one simply
imports from memory to Excel the 2 K record of interest, and then responds
to prompts generated by the chart ``wizard". The abscissa values (time) are
integer ·Dt where Dt
= 30 s/2048. In addition to the obvious difference between the decay constants
in the two cases of Fig. 3, one can also see that the period of the motion
is slightly greater when the can contains glycerin. As compared to the huge
difference in damping coefficients, the variation with period is second order,
as previously mentioned. To produce the reference decay, brass weights were
fixed inside an empty can (56 g mass), the amount selected to approximate
the mass of a water filled can (510 g). The log decrement in this reference
(5.0 (+/-) 0.4×10-3, R2 =
0.993) is evidently influenced largely by the knife edges. By contrast,
the empty can (8.1 (+/-) 0.9×10-3,
R2 = 0.998) is evidently influenced primarily by the
viscosity of surrounding air.
The decay constant which is referred to as the log decrement is defined as
where qN and
qN+1 are the displacements of a pair
of turning points of like sign separated in time by one period of the
oscillation.
In a graph which follows (Fig. 6) of pendulum damping versus viscosity, the
reference damping was subtracted from the measured damping to yield the internal
friction part. Only at low values of the damping was this correction significant.
4 Theoretical Model
The system was modelled by two coupled differential equations:
|
..
q
|
+ c·h1/2 ( |
.
q
|
- |
.
qL
|
) + q =
0 |
|
(2) |
|
..
qL
|
=
h1/2 ( |
.
q
|
- |
.
qL
|
) |
|
(3) |
where q is the angular displacement of the can,
and qL is associated with the liquid
in an ``effective" sense. The constant c is the one adjustable parameter
in the model, and h is the viscosity. Being concerned
primarily with trends in the damping versus viscosity, the term that would
normally multiply the term in q has been set to
unity. Thus the period of oscillation of the model system is 6.28 when
h = 0, rather than the actual experimental
period in the neighborhood of 0.45 s.
The model equations were first tested in a limiting simple case; i.e., by
removing the q term in Eq. (2) and noting that
[(q)\dot] and
[(qL)\dot] approach a common value
exponentially, with a time constant inversely proportional to
h1/2. To solve (2) and (3) numerically,
they were first rewritten as an equivalent coupled set of four first order
equations:
|
.
L
|
=
-ch1/2 (L - LL) - q |
|
(4) |
Although the liquid motion is undoubtedly complicated in most cases, a
simplifying assumption has been made-that the effective angular momentum
of the liquid, LL =
[(qL)\dot] in this ``normalized"
model, is proportional to h1/2. This
assumption is based on comparisons of theory and experiment with rotating
liquids [5].
5 Numerical Technique
The equations of motion (4)-(7) were integrated, using QuickBasic, by means
of the last point approximation (LPA) [6].
The author has used this algorithm instead of Runge Kutta or other techniques
since the 1980's. Even in celestial mechanics calculations performed for
orbital rendezvous and antisatellite intercepts, the LPA was found to be
quite acceptable insofar as errors, and much easier to both understand and
implement than the algorithms traditionally known to the computational physics
community. Careful comparative studies over the past decade by graduate students
under the direction of Prof Tom Gibson at Texas Tech University, have shown
that the LPA is also unsurpassed in terms of code size and CPU times for
execution. The most common use of LPA has been for systems described by fewer
equations than the present pendulum, even though the previous equations involved
nonlinear terms necessary to produce chaos[7].
A testament to the prowess of LPA in the present modelling is the following
observation: When Eqns. (4)-(7) were integrated (single precision) with
approximately 20 widely distributed values of h,
and the turning points fitted to an exponential; the R2 of the
resulting fit was in every case unity according to Excel-meaning a perfect
fit to within at least 4 significant figures. This was true for a particular
value of the time step, Dt, and the essential
(uncommented) code which was used is supplied in Table I.
Table I. QuickBasic LPA code to integrate Eqns. (4)-(7).
(The viscosity parameter is set to h = 1.0,
corresponding to glycerin).
SCREEN12
VIEW (0, 0)-(600, 470)
WINDOW (0,-1)-(1,1)
L = 1: LL=0: th=0: dt = .005
eta = 1.0
start:
t = t + dt
L = L - th*dt - .16 sqrt(eta) * (L - LL) * dt
LL = LL + sqrt(eta) * (L - LL) * dt
th = th + L * dt
PSET (.01 * t, .5 * LL), 2
PSET (.01 * t, .5 * L)
GOTO start
STOP
It should be noted that the integration of LL (LL in the code)
to obtain qL is not performed since this
variable was not used. To estimate the log decrement, whether of experimental
data or of output from the code of Table I written to a file (write statement
not indicated in the table), a QuickBasic software program was produced to
identify the turning points of the damped sinusoid. The peak-to-peak amplitude
of the motion, which is the absolute value of the sum of adjacent turning
points of opposite sign, was then plotted vs time expressed in half-cycle
integers.
6 Model Features
Before considering a detailed theory of the pendulum, it was clear that the
log decrement would exhibit a maximum at some midrange value of the viscosity,
since the damping mechanism must depend on relative rotation of can and liquid.
At very high viscosity, the ``liquid" is fully coupled to the can, and the
absence of relative motion eliminates damping. At very low viscosity there
is maximum relative rotation but the absence of coupling prevents exchange
of energy.
6.1 Model parameter variations with
h
Using Eqns.(4)-(7), the phase and amplitude features of the liquid were
determined as a function of h. As used here, phase
is the angle with which the liquid's angular Momentum
[(qL)\dot] lags behind that of the can,
[(q)\dot]. ``Amplitude" is is the value of the first
peak of [(qL)\dot], obviously influenced
by the initial conditions; which were in all cases
q = 0 = LL and L
= 1. The results are shown in Fig. 4, where the phase is seen to decrease
with increasing h, from an initial value of 0.25
(×2p).
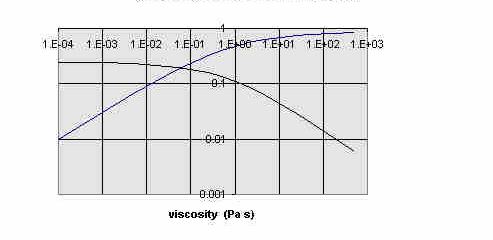
Figure 4. Phase and amplitude of liquid angular momentum vs
viscosity.
It should be noted that an increase in amplitude of
qL (toward 1 as
h®
¥ in Fig. 4) corresponds to a decrease in relative
motion between can and liquid.
6.2 Period
The period variation was not compared directly with experiment for this study;
however, the model does predict that it should increase by
» 8 % as h increases
from 10-3 to 103, as illustrated in Fig. 5.
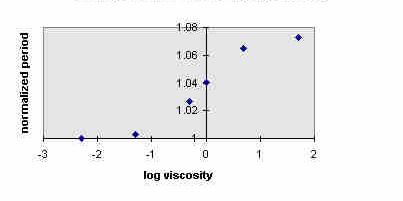
Figure 5. Variation of normalized model period with viscosity.
7 Comparison of Theory and Experiment
To compare theory with experiment, the value of eta in the model code was
set at the viscosity appropriate to the liquid considered (value shown in
Table I being h = 1, corresponding to glycerin).
A record was then written to memory (every 10th point, separated in time
by 0.05), which could be compared to the corresponding experimental record
for that liquid. In all cases, the log decrement was computed by first finding
the turning points in a given record. Then the peak-to-peak values were computed
as previously indicated. Finally, an exponential fit to these peak-to-peak
values was generated using Excel, from which the log half-decrement was obtained
as the coefficient in the exponential fit. For the model sets,
R2 = 1 in all cases as noted previously. The experimental
data typically showed some amplitude dependence to the decay constant, but
R2 > 0.93 in all cases. The liquids
which were considered in this study are indicated in Table II.
Table II. Liquids considered in the study.
Liquid Viscosity (Pa·s)
Mass Density (g/cm3)
Acetone
3×10-4
0.79
Water
1×10-3
1.00
Sugar water
7×10-3
1.02
Vegetable oil 9×10-2
0.86
Mineral oil
1×10-1
0.82
Glycerin
1×100
1.26
Corn syrup 3×100
1.28
Honey
1×101
1.30
Corn starch 1×103
1.03
The sugar water was made by dissolving 40% by weight of sucrose in water
to produce a handbook listed viscosity of the indicated amount. All values
of viscosity less than or equal to that of glycerin in Table II were obtained
from handbooks. The value of h for liquids of higher
viscosity was estimated relative to that of glycerin, using Stoke's Law.
A small steel sphere was dropped in a test tube full of the liquid and the
descent time was measured with a stopwatch. This time was then compared against
the fall time using glycerin.
It should be noted that h is sensitive to temperature
and therefore all experiments were performed at a laboratory temperature
close to 23 C. In addition to the viscosities, the densities of the liquids
are also provided in Table II. These were estimated from mass and volume
measurements and their uncertainty is » 3%.
For an ideal comparison of experiment and present theory, all liquids would
have the same density, which is not possible. This complication will be discussed
later. Theoretical damping (solid curve) is compared against experiment (data
points with error bars in the log half-decrement) in Fig. 6.
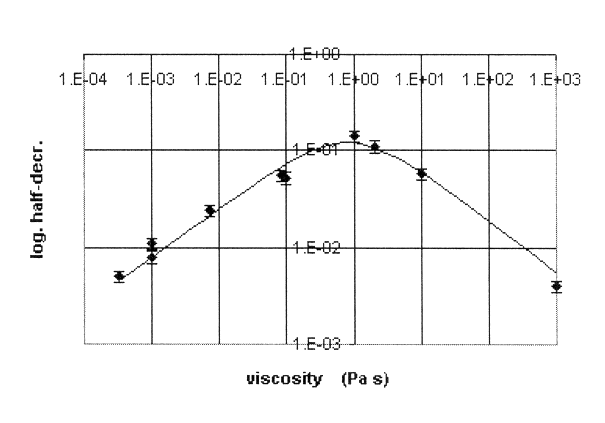
Figure 6. Damping vs viscosity-Comparison of theory and experiment.
For this graph the single adjustable parameter of the model, c of Eq. (4)
was set to 0.16-the value which was found by trial and error to give the
best agreement with experiment. The
(+/-) 16% 1s uncertainty (error bars of
Fig. 6) is based on careful measurements done on glycerin, corn syrup, and
the sugar water, using a set of 24 different records in each case. The range
of the results for the three was from 14% to 17%, and smaller sample statistics
with the other liquids suggested that an uncertainty of 16% is fairly
representative of all cases. The uncertainty in h
is much harder to quantify, particularly for the corn starch, which may be
non-Newtonian. The estimate of its value at 1000 Pa·s could be
wrong by as much as 50%. For the other liquids, the uncertainty in viscosity
is probably in the neighborhood of 20%. In Fig. 6 two points are shown for
water, to emphasize that there is amplitude dependence to the damping in
this experiment. The larger value of the log half- decrement was obtained
with the pendulum oscillating at a ten times larger amplitude. It was also
noted that the R2 declined from 0.99 for the least viscous liquids
to 0.94 for the most viscous ones.
7.1 Influence of mass density differences
In the model, the mass of the pendulum has been assumed constant from one
liquid to the next, which clearly is not true. The invariant quantity being
the volume of the liquid, and since the can mass is only about one-tenth
the liquid mass; we estimate from the densities of Table II that the mass
of the acetone pendulum is » 80% that of water
and that of the honey pendulum is » 130% that
of water. These are the extremes of the variation for the liquids used in
the present study. Future studies will consider whether the kinematic viscosity
would be the better variable with which to make the comparison; i.e., division
of h by the mass density. This seems reasonable
since the damping constant, for a given viscosity, should decrease with
increasing mass. Moreover, the kinematic viscosity is routinely used instead
of absolute viscosity in engineering comparisons of gases. For the data of
Fig. 6, the difference between the graph given and one based on kinematic
viscosity is not great enough to warrant redrawing the figure. A significant
reduction in the viscosity uncertainties, however, would make this meaningful.
8 Use of the can-pendulum as a viscosimeter
The reasonably good agreement between theory and experiment suggests that
the system may be used as an instrument for measuring viscosity. Most liquids
for which one would want to measure h are less viscous
than glycerin. Therefore a power law fit to the low viscosity segment of
Fig. 6 was performed. The resulting R2 = 0.986 is not outstanding,
but still close enough to unity that » 20%
estimates in h should be possible from measured
log decrements , by inverting the expression: log half-decr. =
0.145h0.3936, h < 1. Note that the log half-decrement has been used
in these graphs, rather than the log decrement. To get the latter from the
former, one need only multiply by a factor of 2.
9 Conclusions
It has been shown that some features of a liquid-filled can-pendulum can
be readily understood, whereas others may be so complicated as to defy simple
explanation. Pedagogically, it appears to be a system that is rich in new
possibilities for improved teaching the old physics of classical mechanics.
Particularly when the fluid of the can is inhomogeneous as by mixing solid
particles with a pure liquid, unexpected behaviour can result. For example,
it appears that dynamic organization of particles can then occur for some
conditions, the nature of which are not yet understood. Planned future studies
will attempt to understand these peculiar features. Future studies will also
deal with the importance of pendulum mass, as well as size of the can. The
theory which motivated the h1/2 feature
in Eqns. (4) and (5) also predicts that the dimensions of the can are important
to the damping. Thus, an obvious follow-on experiment would be one to verify
the functional dependence on can diameter.
References
-
[1]
-
R. D. Peters & Tim Pritchett, "The not-so-simple harmonic oscillator",
Amer. J. Phys. 65, 1067-1073 (1997).
-
[2]
-
G. D. Nickas, "Reversing relative displacement in rolling fluids", Amer.
J. Phys. 57, 907-912 (1989).
-
[3]
-
P. Bak, C. Tang, & K. Wiesenfeld, "Self-organized criticality", Phys.
Rev. A ;98, 364- 374 (1988).
-
[4]
-
R. D. Peters, "Capacitive angle sensor with infinite range", Rev. Sci. Instrum.
64, 810-813 (1993). Note: For the present work a single unit with (+/-)
17.5° range was used rather than
the dual unit described in the reference, in which each unit was of range
(+/-) 90°. The electronics
for this sensor may be purchased from TEL-Atomic Inc., Jackson, MI. Alternative
electronics support is described on the WEBpage:
http://physics.mercer.edu/peterpag/sens.htm.
-
[5]
-
H. P. Greenspan, The Theory of Rotating Fluids, p. 4, Cambridge Univ. Press
London (1968).
-
[6]
-
A. Cromer, "Stable solutions using the Euler approximation", Amer. J. Phys.
49, 455-457 (1981).
-
[7]
-
An example is to be found in R. D. Peters, "Chaotic pendulum based on torsion
and gravity in opposition" Amer. J. Phys. 63, 1128-1136 (1995).
File translated from TEX by
TTH,
version 1.95.
On 26 Jul 2000, 09:32.





