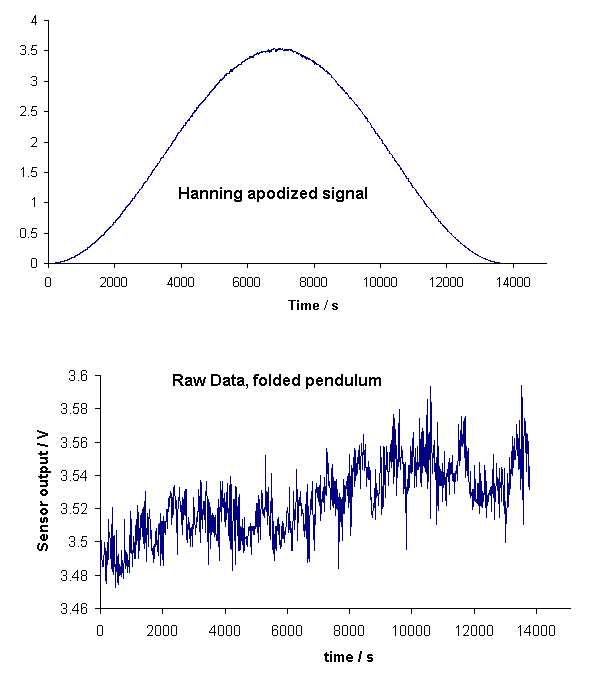
Figure 1. Example of a Hanning apodized record. The data of the lower trace were generated with an open-loop folded pendulum.
The electronics of conventional seismic instruments is a type for which the sensitivity falls off at 20 dB per decade for frequencies below approximately 10 mHz. The frequency response of the instrument is determined by the network characteristics of the force-feedback design. As noted by Wielandt, ``...an output proportional to ground acceleration is unfavourable. .... The system would soon be saturated by the offset voltage resulting from thermal drift or tilt. What we need is a bandpass response ... like that of a normal electromagnetic seismometer ... with a lower corner frequency.''[3].
The sensor of the `normal electromagnetic seismometer' is one which operates on the basis of Faraday's law. The output voltage, determined by the time rate of change of a magnetic flux, is proportional to the frequency of excitation-since a time derivative is involved. We see that the conventional design of modern seismic electronics is cause for severe attenuation of those frequencies corresponding to the most interesting of Earth's eigenmodes. Consider, for example, the lowest frequency case (S2 spherical mode, at 0.31 mHz, corresponding to a period of 54 minutes). For a conventional instrument having a peak response (corner frequency) at 20 mHz, its sensitivity is reduced 60-fold at the frequency of the S2 mode!
For the studies reported in 1 and 2, the electronics was of a different type than that of conventional seismic instruments. These instruments employed a fully differential capacitive sensor [4] in a non-feedback arrangement, resulting in no 20 dB/decade falloff in sensitivity for frequencies below the natural frequency (mechanical) of the tiltmeter. Care must be exercised in such cases, to avoid the saturation tendencies mentioned by Wielandt for this mode of operation.
Although modern seismic instruments use capacitive displacement sensors, their differential arrangement is of a lower symmetry (and thus less sensitive) than those of the `symmetric differential capacitive (SDC) sensor' patented by the author. Additionally, the mechanical range of operation of conventional seismic sensors is severely limited because they function on the basis of gap-spacing variation. By using area variation (a type of `shadow sensor'), much larger mechanical dynamic ranges are possible. Although a large mechanical dynamic range is not important (nor even considered) with the force feedback instrument, it is important for the `open-loop' mode used to see Earth's free oscillations.
Even with adequate sensitivity, it is rare for free oscillations to be plainly visible in `raw trace output' from a typical tilt-sensitive instrument. In the work of ref. 2, autocorrelation was nearly always necessary to see the oscillations. Although autocorrelation analysis is a powerful means for extracting periodic signals from noise, it requires that offset and drift be removed from a record before computing the autocorrelation. This is a laborious operation as compared to the most recent discovery, which is now described.
When doing Fourier transforms (FFT's), the Dataq algorithm permits the
user to select a window (such as Hanning, Hamming,..) with which to
apodize the record. The Hanning window, as an example, is a shifted
cosine of the form H = 0.5+0.5 cos(arg), where `arg' is selected
according to record-length so that
H is zero at both the start and end of the record. The record is
then multiplied by H, as illustrated in Fig. 1.

Figure 1. Example of a Hanning apodized record. The data of the
lower trace were generated with an open-loop folded pendulum.
The maximum number of digital values saved to memory from the A/D converter, for the time span shown in Fig. 1, was 27648 sample points. It is generally inconvenient to do transforms larger than 1024 or 2048 when working with a spreadsheet. Thus the record was compressed by a factor of 27 (by the Dataq software) to yield a reduced total of 1024 points.
There is a significant dc offset in the record, as observed in the bottom trace of Fig. 1. Moreover, the offset increases substantially because of drift in the 14000 s from start to finish of the record. These factors may disallow the detection of any low frequency lines that would otherwise be visible in a spectrum of the raw signal. As will be seen in later analyses of the same record using a spreadsheet, the offset and drift may be readily `subtracted out' before doing the FFT. Such is not necessary when working with spectra only; since the apodized spectrum retains decent low-frequency resolution, as seen in Fig. 2. The reader may find this surprising, since the `useful' information in the top trace of Fig. 1 appears to only `lightly modulate' the shifted (and `amplified') `bell-shaped' cosine apodizer.
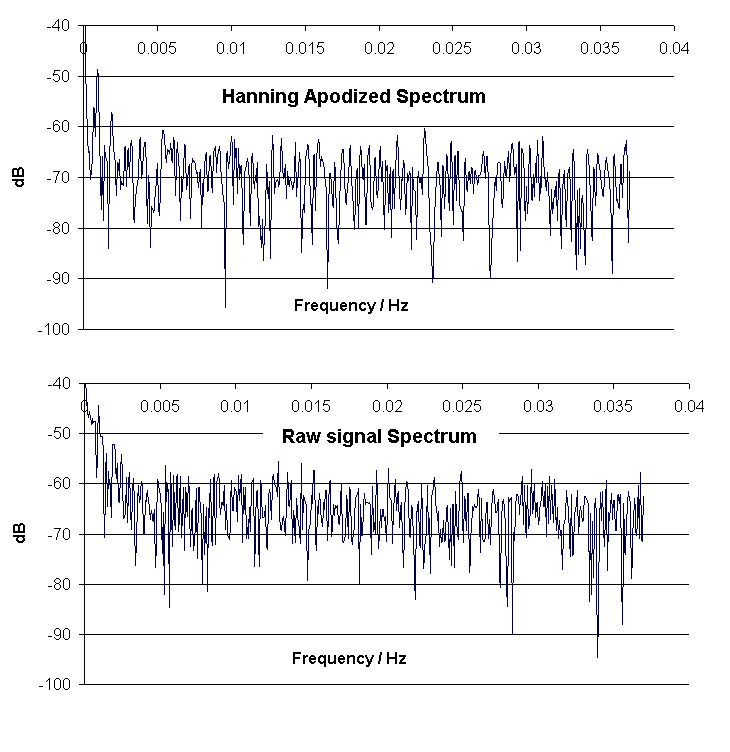
Figure 2. Spectra generated with and without a Hanning apodizer.
When the FFT is taken on the raw data having offset and drift, there is a `shoulder' near zero frequency tending to `mask' the presence of adjacent spectral lines. Thus, Earth's free oscillation spectral line at 0.94 mHz (period 18 min, T5 torsional) is more clear in the top trace of Fig. 2 than it is in the bottom trace computed from the raw data.
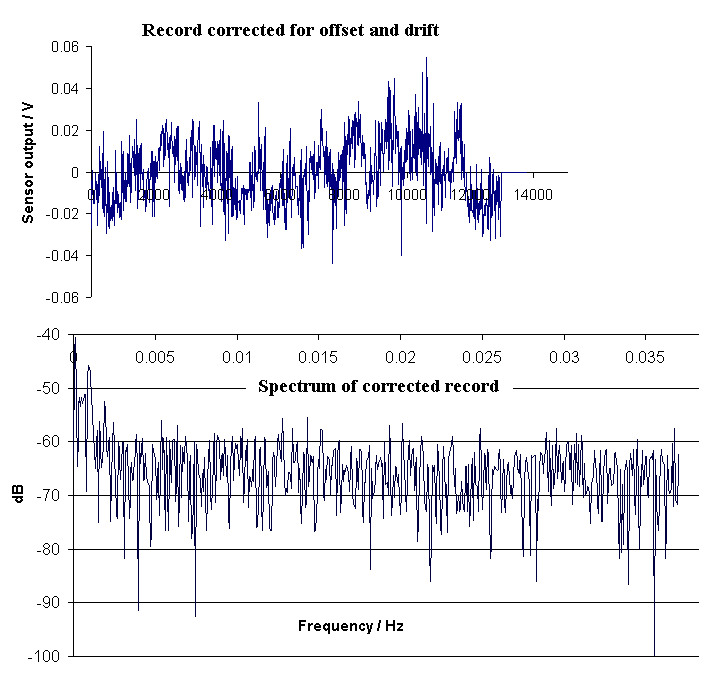
Figure 3. Record and resulting spectrum, after removing offset and drift.
Subtraction of offset and drift was easily done with Excel, and the FFT without apodization of the result (corrected signal) is shown in the bottom graph. The T5 spectral line is still readily resolved in the lower trace of Fig. 3.
Shown in Fig. 4 is the autocorrelation of the 1024 points which constitute
the corrected record (top trace) of Fig. 3. As noted before, a useful autocorrelation
cannot be performed on the raw data (lower trace) of Fig. 1, which
contains offset and
drift.
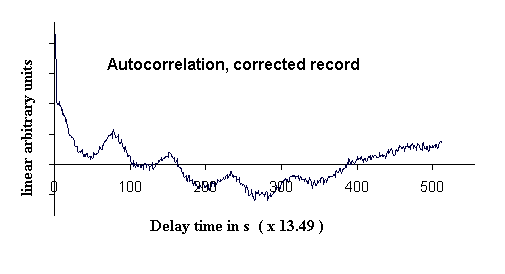
Figure 4. Autocorrelation of the corrected record (top trace) of Fig. 3.
The T5 oscillation of the Earth is readily visible in Fig. 4.
A means for making the periodicity more visible and
reducing the error in a direct estimate of its period, is to operate
on the record
with a bandpass filter
based in a Gaussian `kernel'. A later article will provide details on
how to construct such filters using a spreadsheet.
Shown in Fig. 5 (top graph) is the result
of operating on the corrected record (Fig. 3, top trace) with the bandpass
filter whose
kernel is shown in the lower curve of Fig. 5. The digital signal
processing (DSP, post processing) for this case was accomplished by
means of FFT-based,
spreadsheet convolution.
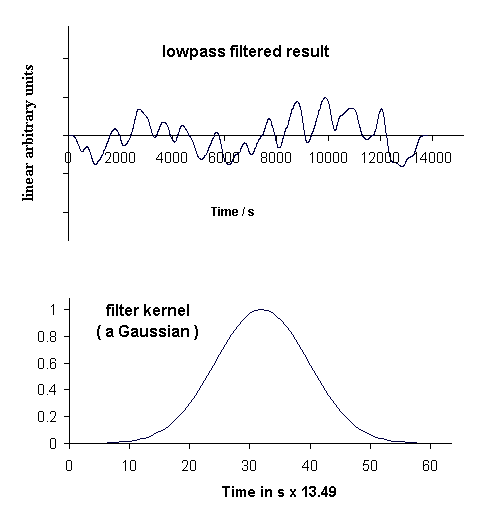
Figure 5. Enhanced direct observability of the T5 mode by means of
a bandpass filter.
Although this paper has concentrated on a single mode, many of the
known (catalogued) spherical and torsional modes of the Earth
have been seen with this instrument over the past two months for which
data has been recorded.
One mode per 24-h record is a rough estimate of the frequency with which
these oscillations have been observed. It should be noted, however,
that their distribution in time is far from uniform. It is hoped
that manpower and time resources will in the future permit
frequency-of-occurrence graphs to be generated and published.
With a period set near 5 s for present purposes, the `background' noise of the instrument is too large for serious earthquake monitoring, because of oceanic microseisms. The period of the pendulum was set at this short value to avoid electronics saturation due to drift. The system is not yet temperature controlled, so thermal expansion and electronics gain change with temperature are responsible for significant diurnal variations in sensor output voltage.
In spite of the above factors, large earthquakes are readily observed, as illustrated in the record of Fig. 6. More important for the present work, and as suggested by the earlier figures of this paper, the instrument is well suited to observation of free oscillations.
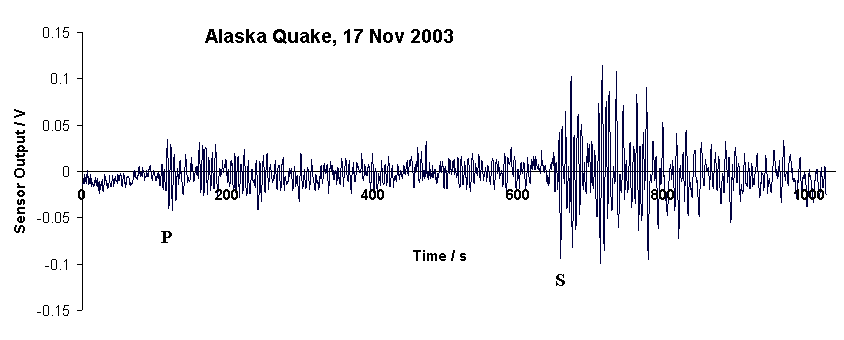
Figure 6. Earthquake record produced with the folded pendulum. The
magnitude of the Rat Island quake was estimated by others to be 7.8 .
Based on the calibration constant noted earlier, the maximum rms amplitude of ground motion in Macon, Georgia due to the quake is estimated around 3 mm. Spectra (not shown) indicate a primary component of harmonicity with a period of about 17 s. The time difference between arrival of the P and S waves of 560 s is consistent with the distance from source to detector, and assumed (nominal) values of P and S propagation speeds.