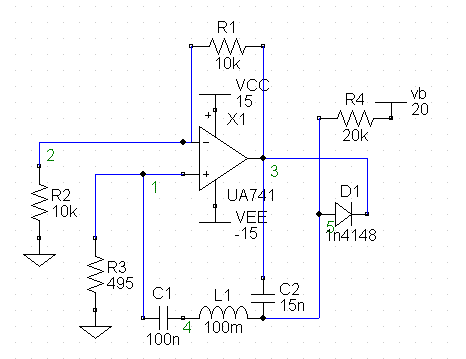
Figure 1. Schematic of the Spice generated circuit corresponding to the Vilnius chaotic oscillator.
Circuit
Shown in fig. 1 is a TopSpice [2] generated circuit. It was
constructed in accord with the information provided in ref. [1],
the paper authored by a
team of researchers at the Semiconductor Physics Institute of
Vilnius University.

Figure 1. Schematic of the Spice generated circuit corresponding to
the Vilnius chaotic oscillator.
Analysis Results
In all of the figures that follow, a single parameter was varied, the
resistor connected between the non-inverting input of the operational
amplifier
and ground. In fig. 1 of ref. [1] this resistor was labeled R; in
the present fig. 1
it is labeled R3 (auto-labeled by the code).
Period-Doubling Route to Chaos
The oscillator shows a period doubling route to chaos as R3 is varied
from 100 ohms to 600 ohms. This is illustrated in the figures which
follow, starting with some time plots in fig. 2. The 100-ohm case (period-1
limit cycle) is
pictured in the upper left graph, and the 600-ohm case (chaotic) is
pictured in the lower right graph.
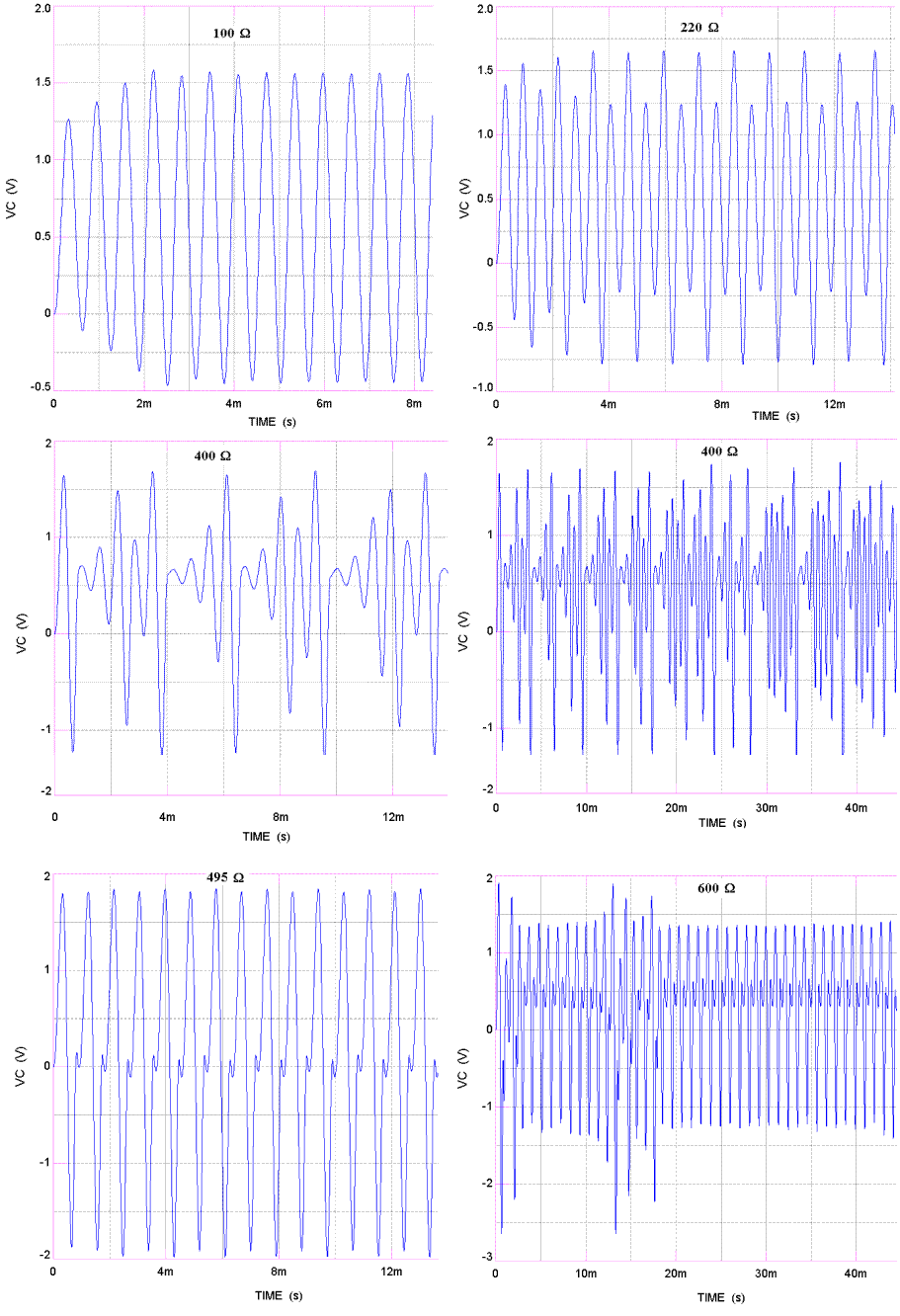
Figure 2. Capacitor C1 voltage vs time for various values of the
resistor R3.
Not all the birucation cases that occur in going from period-1 to chaos are illustrated in fig. 2. For example, the period-2 limit cycle (produced with R3 = 150 ohms), is not included. It looks very similar to the period-4 limit cycle shown (220-ohm case). One must look carefully at this period-4 case (in the vicinity of the lower turning points near -0.25 V) to see that it is not period-2.
The 400-ohm case is chaotic, and in fig. 2 there are two time plots with which it is illustrated. As compared to the left-side graph for this case, the time scale for the plot on the right has been compressed by more than a factor of four. It is worthy of note that the 600-ohm case is also chaotic, but the temporal characteristics of the two cases are seen to be considerably different. In the phase-space plots that follow, the difference between these two chaotic cases is less pronounced.
Phase-space Trajectories
Spice is able to also easily generate phase-space trajectories such as
the right-side-picture of fig. 1, ref. [1]. A similar graph is shown in
the present figure 3 for the R3 = 400-ohm case.
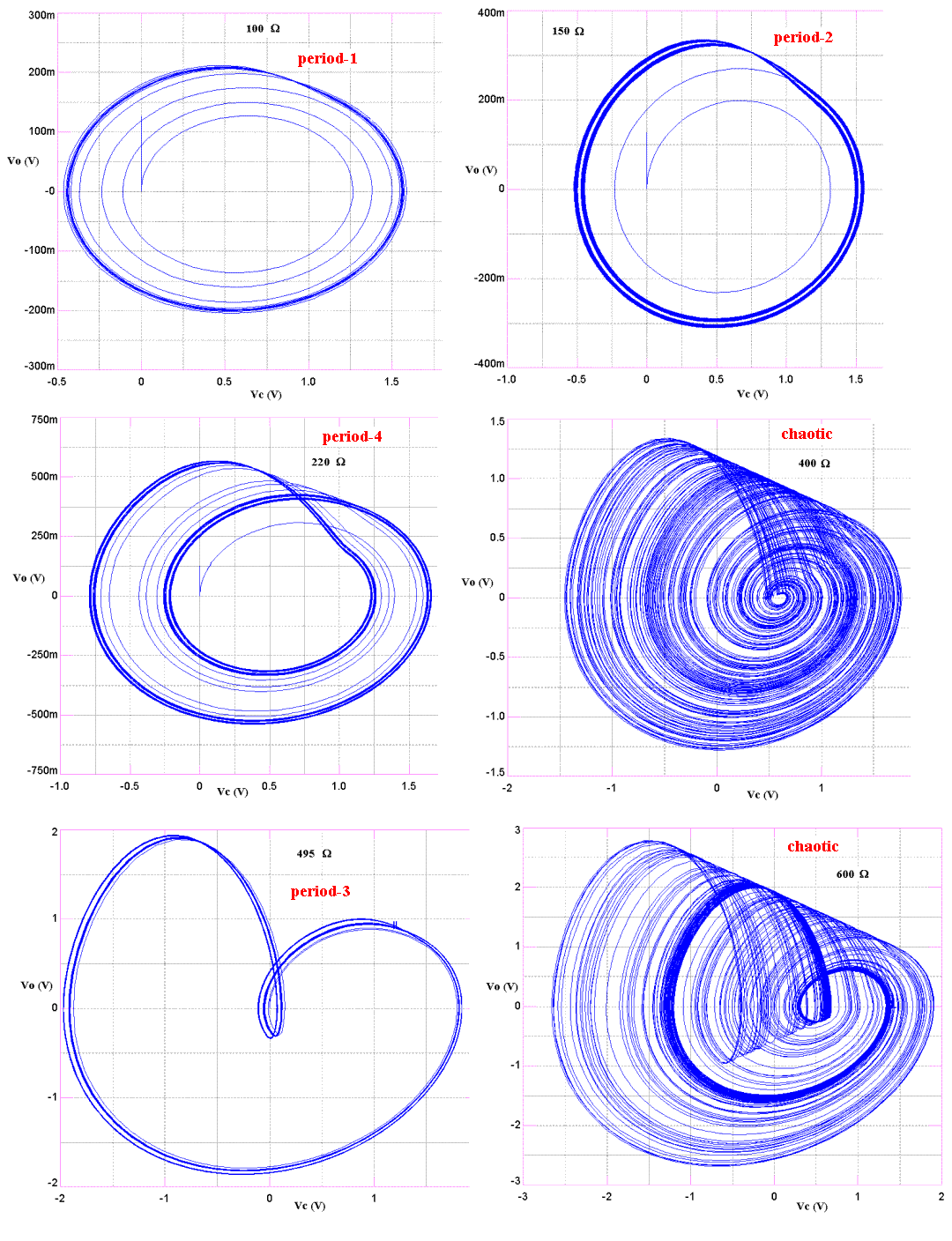
Figure 3. Phase-space plots generated by Spice, that illustrate the
period doubling route to chaos as R3 is varied.
In fig. 3 the first two bifurcations are illustrated at 150 ohms and 220 ohms. Higher-order period-n limit cycles preceding chaos are not presently provided. As seen from fig. 3 the transients have not decayed fully for the periodic cases shown. One must wait still longer for steady state to develop for n > 4, and the author has not yet discovered how to postpone the plot routine for these long transients (assuming such delays are possible).
`Island' in the Midst of Chaos
As with the logistic equation, the Vilnius oscillator shows at least
one period-3
limit cycle located in the midst of chaos (c.f., fig. 2 of ref.[1]).
Presently, it
is the 495-ohm case
of fig. 3. The phase plot suggests period-3, but from the temporal
plot of fig. 2 one could easily mislabel
this limit cycle.
Its true character is plainly evident in the spectum
of fig. 4; i.e., the presence of the 533 Hz subharmonic (1/3 the frequency
of the fundamental for the 100-ohm case).
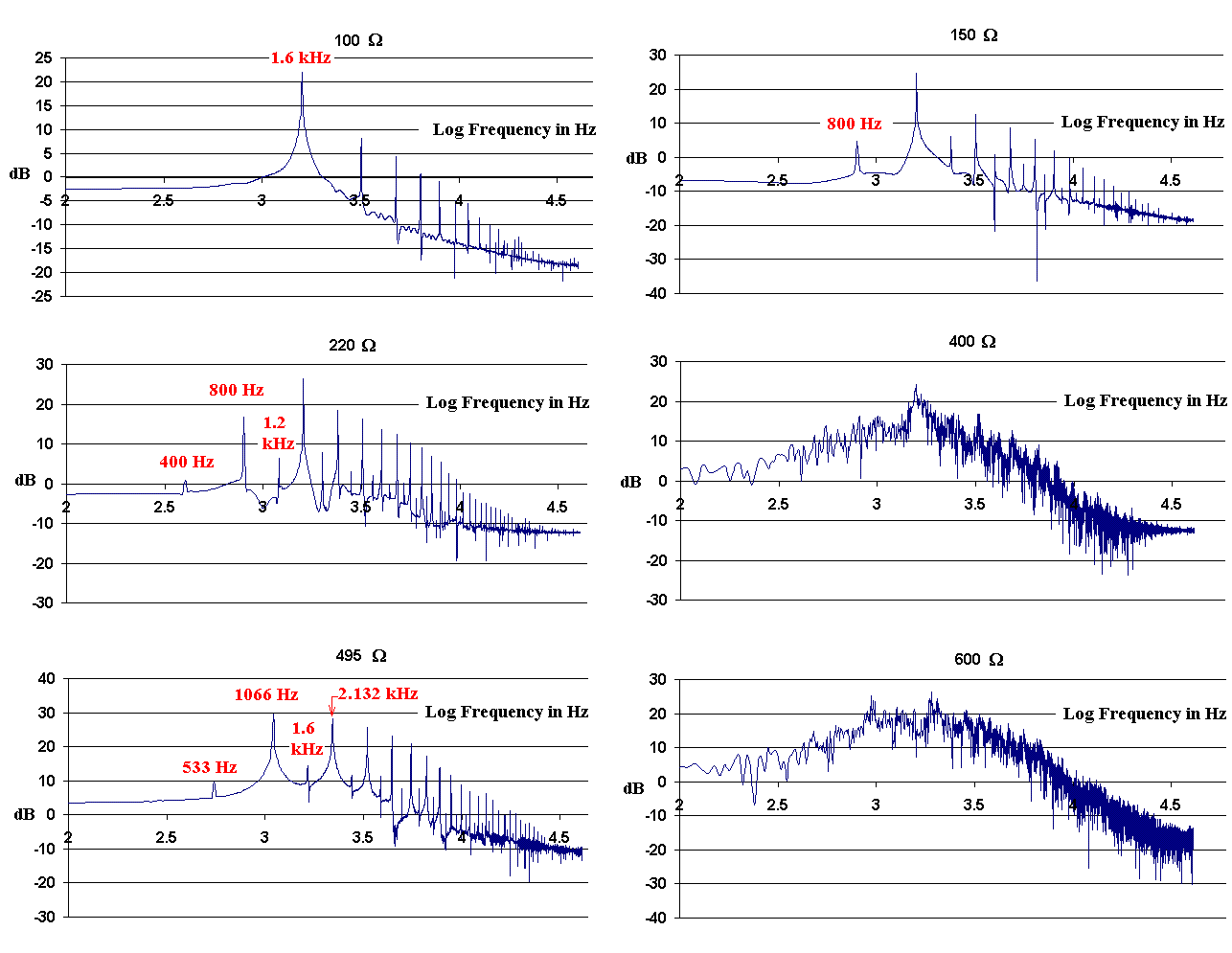
Figure 4. Spectra illustrating the period-doubling route to chaos
and an `island' limit cycle in the midst of chaos.
The hallmark characteristic of the period-3 island (495-ohm case)
is the presence of the 533 Hz subharmonic spectral line.
A not-so-commonly appreciated feature of period-n limit cycles can be observed from fig. 4. The intensity of the subharmonic spectral line which identifies these modes-is never as large as other higher frequency lines. Additionally, note that the period-3 limit cycle is distinctly different in spectral composition than the limit cycles where n is even. In other words the `island' limit cycle is distinctly separate from the ones responsible for the period-doubling route to chaos.
Conclusion
The authors of ref.[1] describe their invention as a `simple chaotic
oscillator'. The present author prefers to go further
by claiming it to be `wonderfully elegant
because of its simplicity'. It thus stands in contrast with other
circuits that have become legendary in the world of chaos.
As demonstrated by means of both hardware and software studies,
the Vilnius oscillator is able to fill an important gap-that which separates
the `maps' preferred by mathematicians (such as the logistic
equation) and the `nonlinear differential
equations' preferred by physicists.
The pedagogical value of this oscillator is significantly increased
because the primary components with which it is built are some of the oldest
elements of modern electronics. As such they have become truly
inexpensive and
readily available the world over.
BIBLIOGRAPHY
1. A. Tamasevicius et al, ``A simple chaotic oscillator for educational
purposes'', Eur. J. Phys. 26 (2005)61-63.
2. The present version of Spice (originally developed at Berkeley
University) is one called TopSpice, available from Penzar
Development. All figures of the present document were generated with
their demonstration version, which is available without cost
at http://penzar.com.