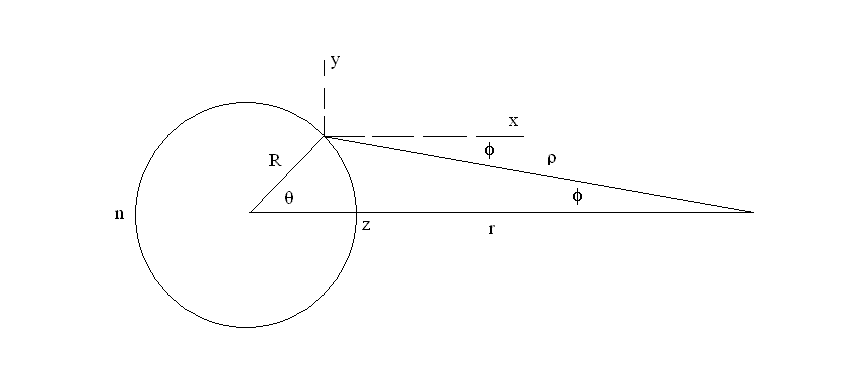
Figure 1. Geometry used to calculate the tidal field.
Randall D. Peters, Marc Erickson, & Louis McNamara
Physics Department, Mercer University
Macon, Georgia
Copyright March 2011
The conventional treatment of the tidal field of the Moon is an approximation that uses calculus differentials, As the distance of a moon from its parent decreases progressively, the assumptions of this first-order approximation become ever more unacceptable. It is then necessary to apply Newton's universal law of gravity to virtually all components of the body. Using codes generated by (i) Excel and (ii) Mathematica, we provide examples of the asymmetry that results from close proximity.
Introduction
The conventional treatment of the tidal field uses only the first derivative of a Taylor series expansion. This treatment defines the tidal force as the gravitational gradient. Consequently, it is a seriously limited approximation for many problems of current interest. Even for the case of Earth, it is shown below that the actual tidal force departs 5% from the symmetry predicted by the historic treatment.
Theory
The foundation for the tidal force calculation is the central force (two-body gravitational) expression used also to derive the laws of Kepler; i.e.,
|
(1) |
where G = 6.67×10-11 N m2/kg2 is the Newtonian (universal) gravitational (fundamental) constant. The common experimental method used to measure G was first described by Cavendish in 1798.
Conventional derivation
The usual method to obtain the tidal force of the Moon (mass m) acting on the Earth (M) is now described. Assume both bodies to be homogeneous spheres. Also, let the Moon be replaced at its center by a point mass of the same magnitude. This is possible by the law of Gauss, which is better known in the context of electrostatics; however, it is also valid for gravity. Next, expand F(r) in a Taylor's series as follows:
|
(2) |
Following evaluation of the derivatives, and after replacing r - r0 with plus or minus R (the Earth radius), the following zenith and nadir estimates for the tidal field are obtained
|
(3) |
Note that in Eq.(3) the subscript zero that was used in Eq.(2) for the distance between centers of Earth and Moon is not being used. This is so r can be treated as an obvious variable-to demonstrate the large asymmetry that results when the ratio of r to R becomes small.
Commonly, only the factor of 1 (first term) in parenthesis is retained. Corresponding to the gradient of the gravitational field, it is sometimes declared to be the definition of the tidal force. By itself, this gradient term predicts magnitude equality for the zenith and nadir components. From Eq.(3) however, it is seen that the 2nd order correction (three-halves the ratio of R to r) causes the nadir part to be 5% smaller than the zenith part in the case of our Moon (where r/R » 60).
Numerical results-Excel
Instead of just the two points of zenith and nadir, described by Eq.(3); a more thorough solution was obtained numerically, using Excel. The coordinate system shown in Fig. 1 was used to calculate the field for points on the circle, throughout the range from q = 0 (zenith) through q = p (nadir), and back to the zenith at q = 2p.

Figure 1. Geometry used to calculate the tidal field.
Using the law of cosines
|
(4) |
which allows calculation of forces in terms of q.
In similar manner, for the parameter relationships evident within Fig.1, one obtains
|
(5) |
The normalized gravitational force components, due to the Moon acting at a point P on the circle of the Earth, are obtained then using Eq.(5) as
|
(6) |
Normalized here means the actual force components are obtained by multiplying the terms of Eq.(6) by G M m.
The algebraic sign of Eq.(6) is chosen for a given point according to the quadrant in which P is located. To obtain the normalized tidal force at P, one then uses
|
(7) |
As prescribed by Eq.(7), the solid curves of Fig. 2 were obtained by subtracting the gravitational field vector at the center of the Earth from each of the vector field values corresponding to 64 points distributed uniformly around the circle of Fig. 1. The ordinate values of the field magnitude (right graph) were obtained through multiplication of fT by the factor R2 / m; so that the tidal field magnitude is an acceleration specified as a fraction of the Earth's gravitational field g = 9.8 m/s2.
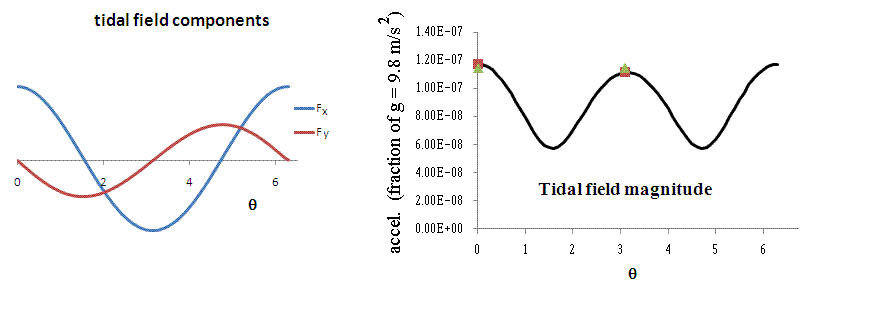
Figure 2. Results obtained numerically using Excel to operate with
the parameters of Fig. 1. The ratio of r/R = 60 corresponds to the Moon's
tidal force on the Earth.
Also shown in the figure are four points-two solid (green) triangles and two solid (red) squares. These two pairs of symbols correspond respectively to (i) the conventional (gradient) tidal force at zenith and nadir, and (ii) what results after using the 2nd order correction terms of Eq.(3). The four points are close enough to the curve that asymmetry is too small to be readily visible, even though the nadir tide is smaller than the zenith tide by 5%.
Asymmetry at smaller r/R
As separation distance decreases, symmetry of the tidal force degrades in a nonlinear manner. As seen from the Fig. 3 example, the amount of asymmetry is dramatic when r/R = 5.
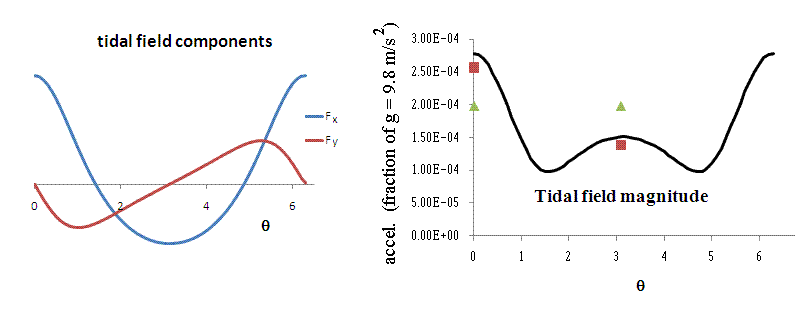
Figure 3. Calculations of the same kind as used to generate Fig. 2,
except now r/R = 5.
The gradient expression for the tidal force is a poor approximation in the Fig. 3 case, as seen from the considerable displacement of the triangles from the curve. The correction through 2nd order [keeping all terms of Eq.(3)] is seen to be substantially better. Nevertheless, at still smaller values of r/R, the full Eq.(3) becomes also increasingly unacceptable, as evidenced by Fig. 4.
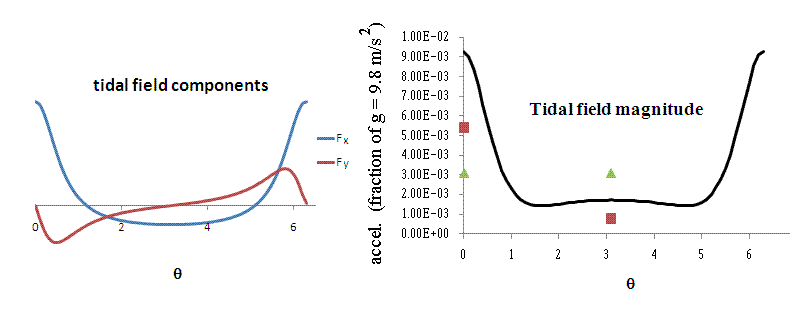
Figure 4. Calculations the same kind as used to generate Fig. 2 except
now r/R = 2.
Numerical Results-Mathematica
Any of the figures 2 through 4 is by itself adequate to describe the tidal force for its given ratio of r/R. Conceptual understanding is enhanced by working also with an alternative means for displaying the same information, but in a different graphical format. It is one that uses a set of arrows to represent the force at selected points around the circle. The length and orientation of a given arrow correspond to the magnitude and direction of the tidal force at the point where the arrow is placed. Although the method has been successfully implemented using Excel, only Mathematica is well-suited to a properly refined output, in which an arrow `head' gets accurately placed on one end of a given `line' that defines the arrow. Shown in Fig. 5 is the case corresponding to the Moon's tidal influence on the Earth. The calculations used to produce the figure are identical with those that were used to generate the curves of figures 2 through 4. Only the display methodology is different.
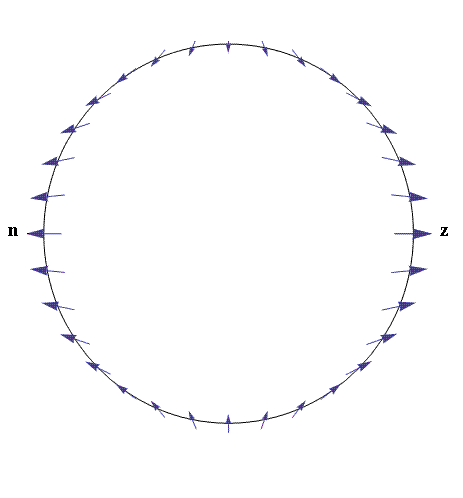
Figure 5. Representation of the tidal force of the Moon on the Earth. Containing
the same information as Fig. 2, this figure was generated with Mathematica.
The obvious asymmetry that is seen in Fig. 3 can also be easily displayed by the same means. The result is shown in Fig. 6.
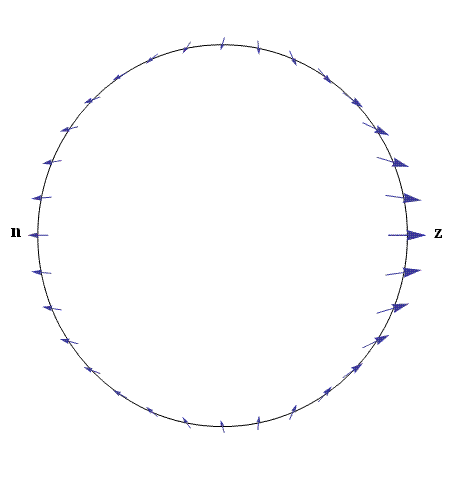
Figure 6. Alternative representation of the Fig. 3 case, showing asymmetry
when r/R = 5.