Ruchhardt Oscillator Decay- Thermodynamic
basis for Hysteretic Damping
Randall D. Peters
Department of Physics
Mercer University
Macon, Georgia 31207
Abstract:
Using thermodynamic arguments based on the ideal gas law, it is shown that
hysteretic (also called structural) damping is the natural form of energy
dissipation for this classic oscillator that is used to measure the ratio
of heat capacities for a gas.
History:
The Ruchhardt experiment is a classic method to measure
g for a gas; i.e., the ratio of heat capacity at
constant pressure to that at constant volume. A typical apparatus for doing
the experiment is pictured in Fig. 1.
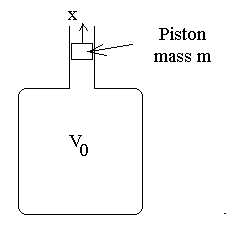
Figure 1. Illustration of the Ruchhardt Apparatus.
The piston of mass m is displaced from equilibrium and released to oscillate
in damped simple harmonic motion. The frequency of oscillation is measured
and this measurement is combined with the known physical parameters of the
system to estimate g.
[1]
Theory:
Consider the piston of mass m moving in a cylinder of cross-sectional area
A, alternately compressing and expanding a volume of ideal gas V0
about the residual pressure P0. Assume that there is no sliding
friction between the piston and the cylinder. This Coulomb friction will
always be present, but the present analysis is concerned only with energy
losses that are internal to the gas.
A small displacement x of the mass results in volume change
DV =
V - V0 = Ax. There is a restoring
force F = ADP, where the pressure difference
DP relates to DV through
an assumed adiabatic process; i.e., the period of the motion is assumed too
short for appreciable heat transfer into and out of the gas. Using
PVg = constant, one obtains
from which
This is the equation of motion of a simple harmonic oscillator without damping.
There is no damping because of the assumed adiabatic process.
By measuring the period
one can estimate g.
Historically, it appears that such measurements slightly underestimate
g, which can be understood as follows. The ideal
gas equation of state PV = NkT yields, through differentiation
which yields
| m |
..
x
|
+ |
P0 A2
V0
|
x = |
NkA
V0
|
DT(t) =
Fd (t) |
|
(5) |
Notice the difference between equations 5 and 2. In 5 damping is possible
(a type of 'negative drive' term) from temperature variations associated
with heat transfer during traversal of the cycle. It it were possible for
the oscillation to be isothermal (DT = 0
at very low frequency, essentially quasistatic), then the frequency would
be lower than that of the adiabatic case, since
g > 1 is
missing from equation 5. In the isothermal case there would also be no damping,
since the heat into the gas during compression would be balanced by that
which leaves during expansion. The only way to get damping is for the paths
of compression and expansion in a plot of pressure versus volume to separate;
i.e., for there to be hysteresis. Reality must correspond to something between
the two extremes of adiabatic and isothermal, with experiment obviously favoring
adiabatic. The process must depart somewhat from adiabatic, however, since
there is damping, which equation 5 shows to derive from temperature variations
yielding hysteresis. It is interesting to look at the temperature variations
relative to a `driving force',
Fd¢(t).
In the Ruchhardt experiment, there must be small variations
DT¢(t) that lag behind
x(t). (These are not the reversible temperature variations of the adiabat,
onto which the
DT¢(t) are superposed.)
By comparing with equation 5, the right hand zero of equation 2 may be replaced
with a damping force that can be written in terms of the velocity as
| Fd¢(t)
µ
DT¢(t) ® - |
c
w
|
|
.
x
|
|
|
(6) |
where c = constant. Notice that the multiplier on the velocity is not simply
a constant, but rather a constant divided by the angular frequency. The use
of velocity is mathematically convenient, but the magnitude of the velocity
(speed) is not expected to be a first order influence on the temperature
changes of hysteresis type. The derivative of x with respect to time not
only shifts the phase by 90 degrees, which accommodates the lag with which
heat is transferred; but it also introduces a frequency multiplier through
the chain rule. Thus to make damping proportional to the velocity would cause
increased dissipative heat flow and thus increased damping as the frequency
is increased. Since this does not happen, and lest we introduce a non-physical
term into the equation, it is necessary to divide by the frequency. Replacing
the right hand side of equation 2 with equation 6 we obtain the modified
equation of motion, with damping
| m |
..
x
|
+ |
c
w
|
|
.
x
|
+ |
gP0A2
V0
|
x = 0 |
|
(7) |
Additional justification for the form of the damping term in equation 7 can
be realized by looking at cases where there is negative damping; i.e., c
< 0. Such is true when the gas is caused to cycle as an engine. An
illustrative case-study was that of a low temperature Stirling engine
[2] in which reasonable agreement between theory
and experiment was realized through the use of an equation based on the same
arguments used to derive equation 7.
It is seen that a straightforward modelling of Ruchhardt's experiment to
include damping yields an equation of motion that is in the form of hysteretic
damping [3] instead of viscous damping. It
appears that for many systems in which the dissipation is dominated by internal
friction, hysteretic damping is virtually a universal form.
References
-
[1] Method described in Heat and
Thermodynamics, M. Zemansky, 4th ed., p 127 (1957). McGraw Hill, New
York.
-
[2] R. Peters, ``The Stirling
Engine-Refrigerator-rich pedagogy from Applied Physics'', online at
http://xxx.lanl.gov/html/physics/0112061.
-
[3] R. Peters, ``Model of internal friction
damping in solids'', online at http://arxiv.org/html/physics/0210121.
