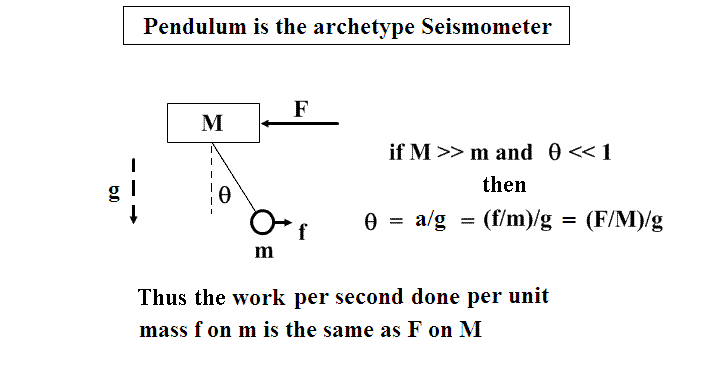
Figure 1. Illustration of a seismometer's response in relationship to the power per unit mass (specific power) of either (i) a segment of the earth having mass M, or (ii) the inertial element of the instrument having mass m.
Randall D. Peters
Physics Department, Mercer University
Macon, Georgia
Copyright October 2007
Theory
A seismometer responds to acceleration of the ground on which it rests, according to Fig. 1, and the specific power (power per unit mass) is calculated as shown in Fig. 2.

Figure 1. Illustration of a seismometer's response in relationship
to the power per unit mass (specific power) of either (i) a segment
of the earth having mass M, or (ii) the inertial element of the
instrument having mass m.

Figure 2. Defining relationship for specific power.
Equation (0) is used to calculate the Power Spectral Density (PSD) corresponding to a seismometer-generated temporal record. The quality factor of the instrument is nominally close to the critical damping value of 1/2 (0.8 being ideal). The earth's field is g = 9.8 m/s2, and q0 is the radian (dimensionless) amplitude (pendulum displacement) due to the harmonic-drive acceleration having angular frequency w = 2 p f
For frequency f of drive higher than the eigenfrequency f0 of the instrument, equation (1) must be corrected according to the following transfer function:
| (1) |
It should be noted that the units associated with p are m2/s3. Eq. (0) is used to calculate the PSD by replacing q02 with the square of the Fast Fourier Transform (FFT) of q0 and dividing by TF2, The units associated with this result are most readily understood when plotted using a linear-frequency scale. Such a linear graph (which is useless except when viewing a small range of frequencies), has units of W/kg per Hz. It should be noted that this is not the same as m2/s4 per Hz. Adjacent points in the plot are separated by Df = FN/(n/2), where FN is the Nyquist frequency and n is the number of points used to compute the FFT.
Most PSD's cover several decades of frequency, so a log-scale is essential. The specification of ordinate units for a spectral density graph involving log-frequency abscissa requires a correction for frequency `compression', when stated as some fraction of a decade or octave. The amount of compression increases linearly with frequency, and this compensates the reciprocal frequency term in Eq.(0). Therefore, simply plotting the square of the FFT of estimated acceleration yields the proper frequency dependence.
Sound-system experts clearly understand from experience the compression phenomenon just described. They refer to 1/f (pink) noise as having equal power per octave, whereas white noise (1/f0) has `equal power per Hz'.
A common practice among engineers is to call spectral `power' the square of the FFT of any quantity whose transform can be calculated. This `bad-science' nomenclature has resulted in enormous confusion, and the practice ought to cease.
A useful PSD convention would be one of dB relative to m2 s-3 per 1/4 th decade, which is essentially also the same as per octave. Its utility derives from the fact that no multiplicative correction to Eq.(0) is then needed. A correction offset of -2.4 dB is required when using the density specification of 1/7 th decade, corresponding to the bin width employed in a well known study of earth noise [1]. In this article, the bin width of 1/7th decade is not specified directly in the dB statement, but is supplied in the body of the paper. It should be noted that m2/s4 per Hz is not a proper set of units for such a graph. Nor is it ever a proper specification for specific power, which has rigorous physical meaning according to Eq.(0).
Vibrational Power of the Earth based on PSD averages
If the preceding arguments are valid, then a profound, yet simple estimate for earth's vibrational power can be realized from the use of a PSD global average-after one more assumption-that the attenuation of all the modes of the earth is similar to the single mode of the seismic instrument; i.e., close to critical damping.
For this calculation we assume for our global-average PSD the `middle' of the observations for the horizontal component only of reference [1], i.e, Fig. 7, for which an approximation has been given in the left graph of Fig. 3 below. (Note that it is here plotted vs frequency, whereas the reference plot is vs period.)
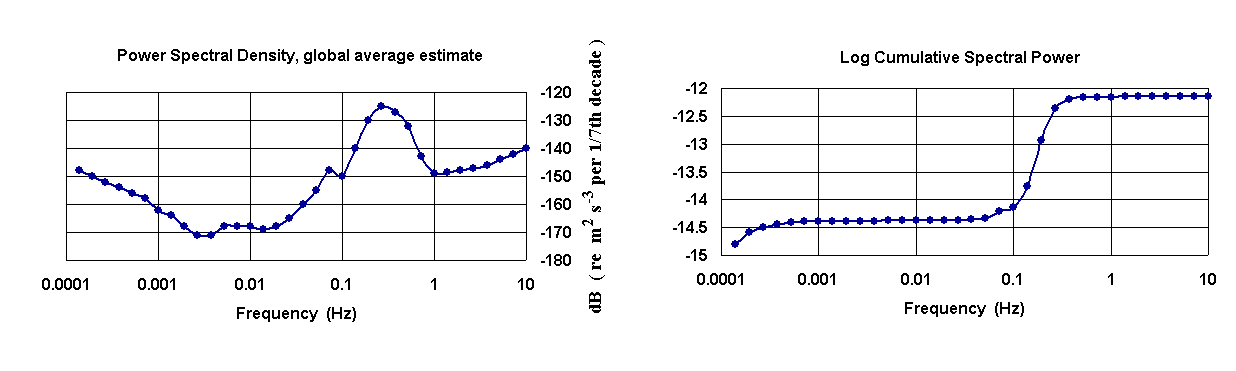
Figure 3. Estimate of a `global-average' PSD for the earth (left
graph), and its associated Cumulative Spectral Power (CSP) (right graph).
The CSP was obtained from the PSD by integration [2]. Its largest value approaches 1. × 10-12 W/kg. We use this number to estimate the earth's average vibrational power in the frequency range corresponding to the graphs of Fig. 3; i.e., about 0.1 mHz to 10 Hz. For the assumptions that have been described, we simply multiply this number by the mass of the earth to yield
| (2) |
It is useful to compare this result to the solar power to which the planet is continually exposed. Assuming 1000 W/m2 and for the radius R = 6.4 ×106 m, one obtains » 1017 W. In other words, the vibrational power for the range indicated is about 0.01 % of the solar power incident on the Earth.
Bibliography
[1] J. Berger & P. Davis, J. Geophys. Res. Vol. 109.
B11307 (2004).
[2] R. Peters, ``A new tool for seismology-the Cumulative Spectral Power'',
online at http://physics.mercer.edu/hpage/CSP/cumulative.html
Note: The values for CSP of this article
are in error. The Log-numbers should be
increased everywhere by a factor of 4.9, since the power spectral
densities on which
they are based
were defined per spectral point instead
of per Hz as was assumed.