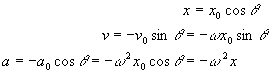
Period of the Simple Pendulum using Elementary Mathematics

Randall D. Peters

Department of Physics

1400 Coleman Ave.

Mercer University

Macon, Georgia 31207

Copyright Oct 2002

ABSTRACT-- The period of the simple pendulum is obtained from considerations of kinematics without using calculus.

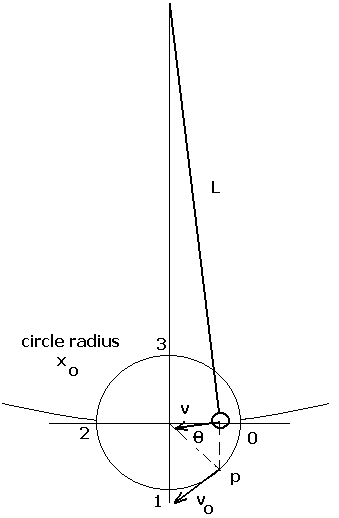
Referring to the figure, consider the circle on which p moves at constant speed, centered on the equilibrium point of the pendulum. Four cardinal points of the particle's motion are indicated by the integers 0, 1, 2, and 3. Zero corresponds to t = 0, followed by points separated in time by one-quarter period. At any given time, p is located by drawing a vertical line through the center of the bob and finding its intersection with the circle. For the position shown in the figure, p is about 1/8 of a cycle from the starting point 0.

Whereas a similar construct is commonly used to describe only position, here we will describe all three kinematic variables x, v, and a--corresponding respectively to position, velocity, and acceleration of the pendulum bob. These variables are one-dimensional vectors, in which direction is determined by algebraic sign relative to the horizontal x-axis onto which all projections are made. In the figure, only velocity vectors are shown, one for the circular motion (constant magnitude v_o), and the other for the pendulum motion (variable magnitude v).

Insofar as p is concerned, there are two invariant quantitities, the magnitude of the particle's velocity v_o and the magnitude of its acceleration a_o. To obtain the period of the pendulum in terms of its length L and the acceleration of gravity g, we must specify v_o and a_o in terms of the period T, which is readily done. The speed is simply the circumference of the circle divided by the period of the motion; i.e., v_o = 2px_o/T = w x_o . The acceleration is centripetal and the magnitude is given by a_o = v_o²/ x_o = w² x_o . (It is worth noting that many introductory physics textbooks develop this expression for centripetal acceleration without employing calculus.)

Looking at the figure, one can see that the pendulum's kinematics is obtained from the particle's kinematics through the expressions

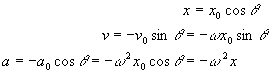
which are valid only if x_o << L.

To get the period of the pendulum in terms of L and g, we must now (finally) employ Newton's 2nd law S F = m a. The net force is the restoring one in the -x direction ; i.e., S F = - mg x / L = m a = -mw² x . Thus we obtain w² = g / L, yielding the desired result

without having to do any calculus whatsoever.