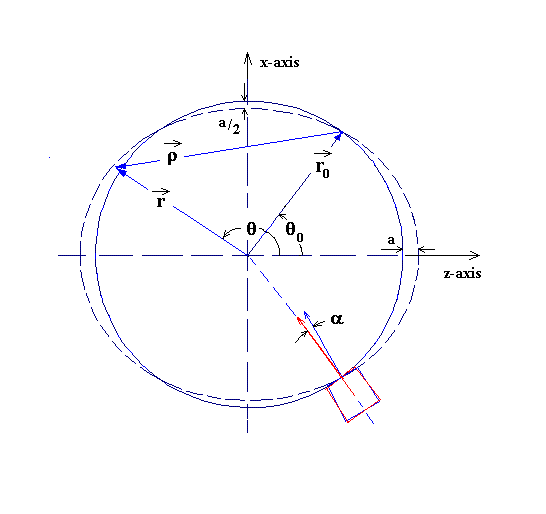
Figure 1. Illustration of the lowest frequency, commonly-excited mode of Earth vibration.
Abstract
One of the best ways to measure low-frequency
eigenmode oscillations of the Earth is to monitor a simple pendulum
responding to tilt. A theoretical basis for the method
is given, by investigating a particular, well-known
standing wave-the one with 53 minute period
corresponding to oblate/prolate spheroidal deviations from the
geoid.
The first observation of frequently-occurring oscillations with similar mHz frequencies was by Kwon and Peters nearly two decades ago [2]. Unlike the modes following large earthquakes, these real-time observations were concerned with oscillations having much shorter lifetimes, and which are therefore much less monochromatic. Later analysis of superconducting gravimeter data discovered related oscillations which have come to be known as incessant `earth hum' [3].
For many years now the ordinary pendulum has been viewed only as a reference against which the performance of ``superior'' seismographs are `quantified'. Experiments by this author have shown this to be a serious oversight [4].
The simple pendulum responds not only to `acceleration devoid of tilt' but also to `tilt devoid of acceleration'. In either case it is responding to the ONLY thing that causes motion in ANY seismometer; i.e., acceleration. In the case of tilt, it is the component of the earth's field that is perpendicular to the case of the instrument. Einstein showed through the equivalence principle that these two phenomena are indistinguishable; i.e., one cannot from a localized observation tell the difference between acceleration and a gravitational field.
The tilt response of an instrument, whether it be a simple pendulum or a more sophisticated horizontal seismograph such as the type called `garden-gate', has been long viewed as being afflicted with undesirable noise. It is well known in seismic circles, for example, that the equivalent noise power of horizontal seismometers is in general, significantly greater than that for vertical seismometers. A significant part of this does indeed derive from localized disturbances that hamper earthquake studies. Such localized sources of tilt generally contribute only to `high frequency' components of the seismograph response. The much lower frequency of the eigenmodes being presently considered are not usually observed by seismographs. The sensors of commercial instruments operate on the basis of `velocity' rather than `position' measurement. Differentiation severely attenuates their response in the mHz range which is the focus of this article.
It is shown here that not all variations of tilt-type should be thought of as noise. Free-oscillations of the Earth can excite a pendulum, if the instrument is positioned on a `line-of-nodes' of the standing wave, as we now illustrate.
Consider the oscillation pictured in
Fig. 1. For ease of calculation, the undisturbed (non-vibrating) Earth is
approximated in this
case as a sphere of radius R (magnitude of vector r0).

Figure 1. Illustration of the lowest frequency, commonly-excited
mode of Earth vibration.
The actual geoid departs from spherical by only 0.3 percent, due primarily to the Earth's rotation. Being an equipotential, a plumb bob (static pendulum) hangs in a (vertical) direction that is perpendicular to the geoid. There is no loss in generality by assuming a sphere for the present treatment that is concerned with oscillations about the `geoid'.
In addition to the circle (solid line) slicing through the center of the Earth in Fig. 1, also pictured is a slice of the maximum excursion (dotted line) associated with the vibration. It is the oblate/prolate eigenmode oscillation whose period equals 53 minutes. Interestingly, if the Earth were totally a liquid, bound together by gravity and having the same radius R and same average mass density; then the period would be 94 min.[5].
As in the model of ref. [5], based on spherical harmonics, we here assume that the dotted line deviates from the sphere by the following expression, that corresponds to the Legendre P2 function, involving the polar angle q:
| (1) |
where azimuthal symmetry has been assumed (no f dependence).
The line of nodes for this case is the pair of circles situated at q0 = cos-1(1/31/2) and p - q0. An instrument package is shown positioned at one of these nodal lines; for r0 pointing toward f = 0, the instrument is located at f = p.
As the Earth oscillates, the case of an instrument located on the line of nodes rocks back and forth through a peak-to-peak angle that is twice the following (readily shown after taking the derivative of Eq.(1):
| (2) |
This angle would be the amplitude of the tilt signal observed by the pendulum shown, if the gravitational field were to always point directly toward the geometric center of the Earth.
It is important at this point to understand that there is a dramatic difference between the manner in which a pendulum responds to (i) acceleration devoid of tilt, as opposed to (ii) tilt devoid of acceleration. In case (i) the steady state response amplitude (for position, as opposed to velocity sensing) is proportional to the square of the drive frequency; assuming the well known transfer function for a driven harmonic oscillator with damping, and drive frequency below the natural frequency of the instrument. In case (ii) the transfer function is independent of the drive frequency; i.e., the output is `flat to position'. For a 0.3 mHz drive (frequency associated with the motion of Fig. 1), a pendulum whose natural period is 1 s would have little chance of detecting pure acceleration. As compared to a pure tilt measurement, the output would for this case be attenuated by a factor of eleven million. If the pendulum were operated with a velocity sensor, this attenuation factor would be 37 billion.
A word concerning pendulum length is in order. In the case of earthquakes, the slowest variations observed from teleseismic events (Rayleigh and Love surface waves) correspond to periods rarely in excess of 30 s to 50 s. Their wavelength is too short to provide a signficant tilt contribution to the pendulum's response. In this case, the output is proportional to the square of the ratio of drive frequency to instrument natural frequency. Especially in the days of poor electronics, it was important then to make the natural period of the pendulum as long as possible. For the tilt response which we are presently considering, this is not an issue. It should be noted, however, that friction (especially of internal type [6]) reduces performance as the instrument shrinks in size. This is NOT a phenomenon involving Brownian motion, which is popularly, though wrongly believed to be the culprit.
It should also be noted that, as long as the pendulum is not friction-hindered, neither its length nor its mass is an issue for this type of measurement.
The gravitational field of a body depends on every mass-piece of that body. For a homogeneous sphere, the field at the surface is readily determined using Gauss' law, to be radial and have the surface magnitude g = G M/R2, where G = 6.67×10-11 N m2/kg2 is the Newtonian (universal) constant, and M is the mass of the sphere having radius R. For the Earth, M = 6×1024 kg and R = 6.4 ×106 m. (The reader may readily verify that these numbers yield the value g = 9.8 m/s2.)
With a change from spherical to spheroidal shape, the field at points on the nodal line shifts slightly away from the radial direction. Instead of pointing toward the origin, the field in Fig. 1, at the position of the instrument, is directed toward a point 0 < dz << R. The sensible way to calculate this change in direction is to use a perturbation analysis. As a `deviation' from the spherical case, points of the spheroid that are farther from the origin than R, attract the instrument because of their mass. By contrast, points closer than R are `repulsive'. Using these considerations, a numerical integral was performed. Prior to doing this integral, various vectors were expressed in Cartesian coordinates as follows, involving the unit-vectors i along x, j along y, and k along z:
| (3) |
Consider the differential volume of a perturbing mass element located at position (r,q,f). It is given by the spherical coordinate expression dV = r2 dr sinq dq df, from which the mass of the element is given by 3M dV/(4p R3). This assumes a uniform mass density for the Earth, which should represent a `worst case scenario'. Because the density of our planet increases toward the center, the actual shift should be even smaller than what we're about to calculate.
We use the differential volume to obtain the magnitude of perturbing field due to the differential mass, relative to the spherical Earth's field g, as
| (4) |
Only the component of vector dg¢ that is perpendicular to g is of significance to our treatment, since it is the only component that results in a direction change. Additionally for that component, only the portion lying in the x-z plane contributes to the direction change; since the y-components cancel in symmetric pairs as integration is performed over the azimuthal angle. Thus before integrating Eq.(4), it was multiplied by the product of two trigonometric terms: (i) the sine of the angle between (r - r0) and r0 and (ii) the cosine of the angle that r - r0 makes with the x-z plane.
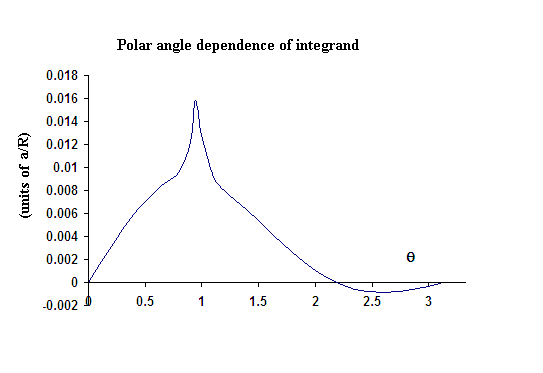
Figure 2. Plot of the integrand for the 2nd numerical integral over
q. The previously-computed 1st integral over f has been
incorporated in the plot.
To obtain the angular deviation of the Earth's field caused by the oscillation, the area under the curve of Fig. 2 was numerically evaluated. The sum yielded the value 0.14 a/R, which is of order one-tenth the angle of instrumental case tilt mentioned previously. In other words, it has been demonstrated that tilt of a pendulum is an effective means for studying the lowest frequency, commonly excited eigenmode.
Note for the analysis just given, that the pendulum is responding to a mode of the Earth that is spheroidal rather than torsional. It is popularly thought that an instrument that responds to horizontal ground acceleration would be insensitive to such a mode. Such reasoning does not account for the most important modus operandus with which a pendulum is able to see the eigenmodes; i.e., tilt response.
A different type of instrument responsive to pure (vertical) acceleration would see the largest signal when positioned at q = 0. Using the value a = 0.01 m as before, the acceleration at that position would be 39 nm/s2.
Although the analysis given in this article was concerned with only a single mode, it is reasonable to believe that for other modes the change in field direction would not exceed one-tenth the case tilt of the pendulum as it responds to the mode. Of course the response requires that the instrument be located on a nodal line of the mode. If a network of pendulums were utilized, it is expected they would be a viable means for studying the Earth's free oscillations over a wide range of mHz frequencies. Experimental evidence for viability of the concept has already been demonstrated from various studies by the author, including that of hurricanes such as Katrina [7].
Bibliography
[1] H. Benioff et al, ``Excitation of the free oscillations of the earth
by earthquakes'', J. Geophys. Res., Vol. 66, 605 (1961).
[2] Documented first in Kwon's PhD dissertation, ``Refinements of New
Balance for measuring small force changes''(p. 71), Texas Tech University
(1990). Later journal-published, M. Kwon & R. Peters, ``The
study of eigenmode types and source nonlinerity in the free
earth oscillations'', Saemulli Vol. 35, no. 4, 569 (1995).
[3] K. Nawa et al, ``Incessant excitation of the Earth's free
oscillations'', Earth Planets Space, Vol. 50, 3-8 (1998).
[4] R. Peters, ``Modernized conventional pendulum seismometer'',
online at http://arxiv.org/html/physics/0508028
[5] J. Trefil, Introduction to the Physics of Fluids and Solids,
Pergamon Press, p. 111 (1975). Note: the period
labeled t2 = 45 min, following Eq. (7.A.18) is a typo that
should read 94 min rather than 45 min.
[6] R. Peters, ``Friction at the mesoscale'', Contemp. Phys., Vol. 45, No. 6, 475-490 (2004).
[7]. R. Peters, ``Earth oscillations induced by Hurricane Katrina'', online at http://arxiv.org/html/physics/0604190