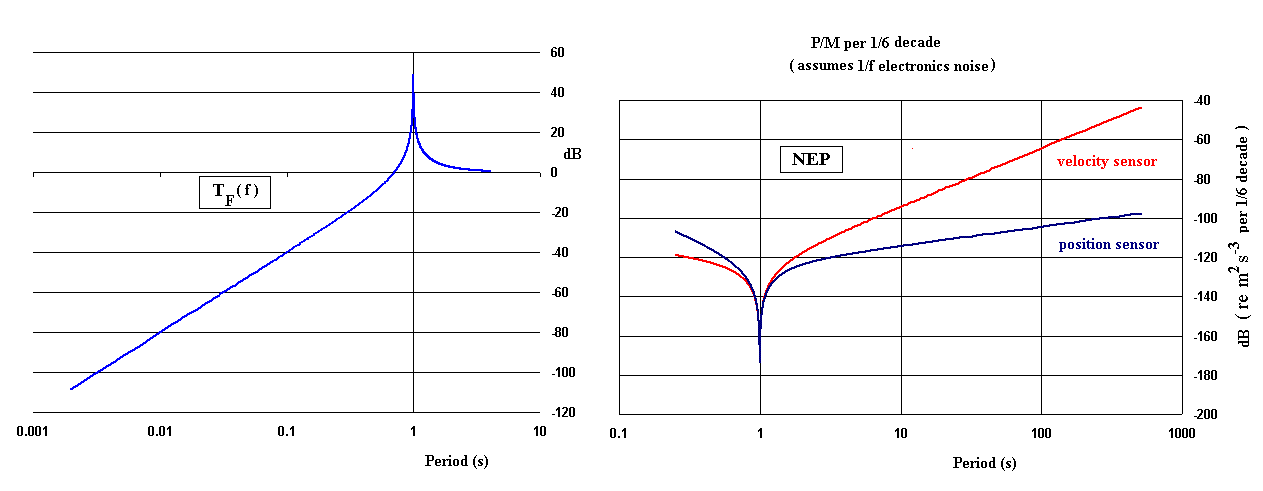
Figure 1. Transfer function and associated NEP for a lightly damped pendulum with Q = 290. A large improvement in NEP is realized at low frequencies when position sensing (blue) is used instead of conventional velocity sensing (red).
Every sensor operates on the basis of energy transfer. Performance is ultimately limited by self-generated power fluctuations. For systems amenable to linear analysis, the influence of these fluctuations is quantified by the instrument's noise equivalent power (NEP). If the concept of NEP was at all employed by previous designers of seismometers, then it appears that the physics was not properly applied.
Before trying to understand the NEP, it is useful to first look at a confusing standard that dominated the seismic community for years.
In keeping with nomenclature that is close to electronics tradition, early seismograph users tried to understand their instruments by working with a plot of ``acceleration power density''. Just as the noise in electronic amplifiers is often specified as `volts per root Hz', so the units of this convention are meters per second squared per root Hz. Because electronics power is proportional to voltage squared, one observes immediately that this noise statement is not one that actually specifies power.
The modern convention for representing what most believe to be always just site noise, as opposed to instrument self-noise, is better but still confusing through retention of the word ``acceleration''. The units in this nomenclature are meters squared per second cubed per Hz. Instead of `per Hz', the numbers on graphs are specified relative to some fraction of a decade of frequencies, for example one-sixth of a decade. The 1/6 decade is convenient because it relates nicely to 1/3 octave, the standard employed by acousticians for years. The units for the numbers thus displayed should really be labeled ``power per unit mass per one-sixth of a decade'', as now explained.
Seismometers respond to acceleration and that alone, even though tilt is thought by the uninformed to be something different. Einstein provided guidance for the naive, if one can comprehend the essence of his equivalence principle. Newton's second law F = M a, involving force F, mass M, and acceleration a --is basis for understanding everything according to linear approximations. Actual instruments are performance limited, expecially at low frequencies, by nonlinear damping that derives from internal friction of their mechanical structures. The author has studied the physics of these nonlinearities for about two decades, but nothing relating to nonlinearity is treated in the present article. What this article does treat is basic classical physics. The author is stunned by the fact he hasn't been able to find any article of similar type, in his extensive search of literature devoted to seismometers. After all, NEP is foundational to the work of practitioners in other science fields, such as optics. There, for example, the author routinely used noise equivalent flux density (NEFD) as a means for determining performance of the sensor employed by the miniature vehicle of the U.S. antisatellite system.
Mechanical power per unit mass of the Earth is what fundamentally regulates the response of all seismic devices. From Newton's second law we recognize this to be nothing more complicated than the following:
|
(1) |
where steady state harmonic motion is assumed for all frequency components; and A represents the amplitude of ground motion, v0 is the amplitude of the ground velocity, and w = 2pf is the angular frequency.
What is not explicitly indicated in Eq.(1) is the frequency dependence of A (and also therefore of v0, since v0 = w A). In keeping with Bode-plot convention of electronic systems, P/M vs frequency (or more commonly, vs period T = 1/f for seismic descriptions), is specified in terms of decibels dB. Because the old standard (acceleration power density) is actually square root of power, its definition of the dB uses 20 times the log (base 10). The newer standard, involving a bonafide power set of units, uses 10 times the log. Thus a change of 40 dB in a graph of the former corresponds to only 20 dB change in a graph of the latter.
Just on the basis of Eq.(1), important features of seismometer performance can be understood without ever knowing the specifics of earth noise. We start by assuming `white' noise for the earth, which simplifies the analysis. If known, actual earth noise can be later easily added, since the output from the instument is the convolution of the two parts (assuming linear equations): (i) instrument self-noise and (ii) earth noise. Due to the properties of convolution, the output is obtained from the product of the two parts, each of which depends on frequency (math in the frequency domain rather than the time domain).
Thus we concentrate on the self-noise of the instrument, labeled NEP; which is a function of frequency f. If at every frequency considered, the NEP of a sensor is greater than the power supplied by the object under study, then there is no way the sensor will detect that object. Simply stated, for this scenario the signal to noise ratio SNR is everywhere less than one. It matters not whether the noise is associated with the environment where the object resides, or if the noise is of NEP type, or both; the object will not be observed unless the noise can be subsequently reduced by some means. One excellent means for reducing NEP is to use synchronous detection, the heart of lock-in amplifiers. With the exception of the first bonafide fully-digital seismograph designed by the author (Volksmeter being readied for commercialization), virtually all modern instruments use this proven method of synchronous detection, which was invented by physicist Robert Dicke. It served Dicke well, who used the method while at Princeton to provide experimental proof for the equivalence of inertial mass and gravitational mass, that is central to Einstein's contribution mentioned earlier. Another effective means is to lower the temperature of electronic components, thus reducing Johnson noise.
The single-most influential factor in the determination of NEP of a seismometer is its transfer function; i.e., the frequency dependent TF(f ) that determines the size of measured amplitude Ameas compared to actual amplitude A that appears in quadratic form in Eq.(1). For the simplest systems, the transfer function is nothing more than the classic, steady state response of the driven simple harmonic oscillator with damping. From the solution to the equation of motion of either a simple pendulum or a mass/spring oscillator (mechanical essence, respectively, of horizontal and vertical seismographs) one obtains the following result:
|
(2) |
where f0 is the natural frequency of the instrument and Q is the quality factor with which it oscillates in free-decay-determined by the amount of damping. Generally, a seismometer operates with Q close to the critical damping value of 0.5, with Q = 0.8 being common.
If the motion of the earth were flat to frequency, meaning an A in Eq.(1) that is independent of f (white noise); and if TF were constant rather than the form shown in Eq.(2), then a dB plot of P/M per one-sixth of a decade vs log of period would be a straight line declining everywhere at 40 dB per decade. Because the frequency appears cubed in Eq.(1), one might expect the decline should instead be at 30 dB. The reason for the additional 10 dB is now explained.
The frequency dependence of a variable is calculated by means of the Fourier transform. Practical calculations use the fast version (FFT) invented by Cooley and Tukey. Adjacent lines in the spectrum are separated in frequency by Df = fmax/(N/2), where fmax = fs/[2(1+2/N)] is the Nyquist frequency, determined by the sample rate fs. The total number of samples is required by the FFT to satisfy N = 2n, where n is an integer, and typically n = 11 or larger for adequate spectral resolution.
The plot of P/M is one of power per unit mass specified as a density; i.e., the amount of P/M per one-sixth of a decade (the NEP). As the frequency increases, the number of spectral line per decade in the FFT also increases. Every ten-fold increase in frequency is accompanied by a ten-fold increase in the spectral line density. Because all lines contribute equally to the power, this increase yields the extra 10 dB per decade.
The most common form of noise in nature exhibits the frequency dependence 1/f in the power. If we assume this instead of white noise for A in Eq.(1), then the decline mentioned above decreases from 40 dB to 30 dB per decade. A decline at this rate is not ridiculously wrong for periods less than about 10 s. For larger periods, however, the trend must at some point stop and then reverse direction.
An understanding of this trend change is found in the nature of the transfer function specified by Eq.(2). For a given frequency f that is well below the natural frequency f0, the sensitivity (¶Tf /¶A)|f µ 1/f02 is seen to fall off with the square of the natural period. This property of mechanical oscillators is well known to seismologists, and it is the reason simple pendulums lost favor about a century ago; since their short natural period results in insufficient sensitivity for the electronics types that have ruled until recently. What designers appear to have missed is the importance of the frequency dependence of TF on the NEP, as illustrated in Fig. 1. The left plot of the graph shows the transfer function, and the right plot is the NEP that results from this TF.

Figure 1. Transfer function and associated NEP for a lightly damped
pendulum with Q = 290. A large improvement in NEP is realized at low frequencies
when position sensing (blue) is used instead of conventional velocity sensing
(red).
The difference in frequency dependence of NEP for the blue and red curves of Fig. 1 can be understood as follows. As seen from Eq.(1), power is proportional to the square of what is estimated by measurement, whether it be position A or velocity v0. But the exponent on w is different for the two; i.e., it is raised to the third power for a position sensor and only to the first power for a velocity sensor. This causes a difference between the two cases of 20 dB per decade, consistent with the known influence of taking the derivative.
If this simple theory of NEP is valid, then clearly the obvious way to dramatically improve performance at low frequencies is to alter the modus operandus that is common to all commercial seismographs; i.e., stop employing velocity detectors and go to the use of position detectors.
Let us consider some systems quite different from the instrument assumed for Fig. 1. We now restrict our attention to instruments that are nearly critically damped, and consider what happens to NEP as the natural period of the instrument is increased, as illustrated in Fig. 2.
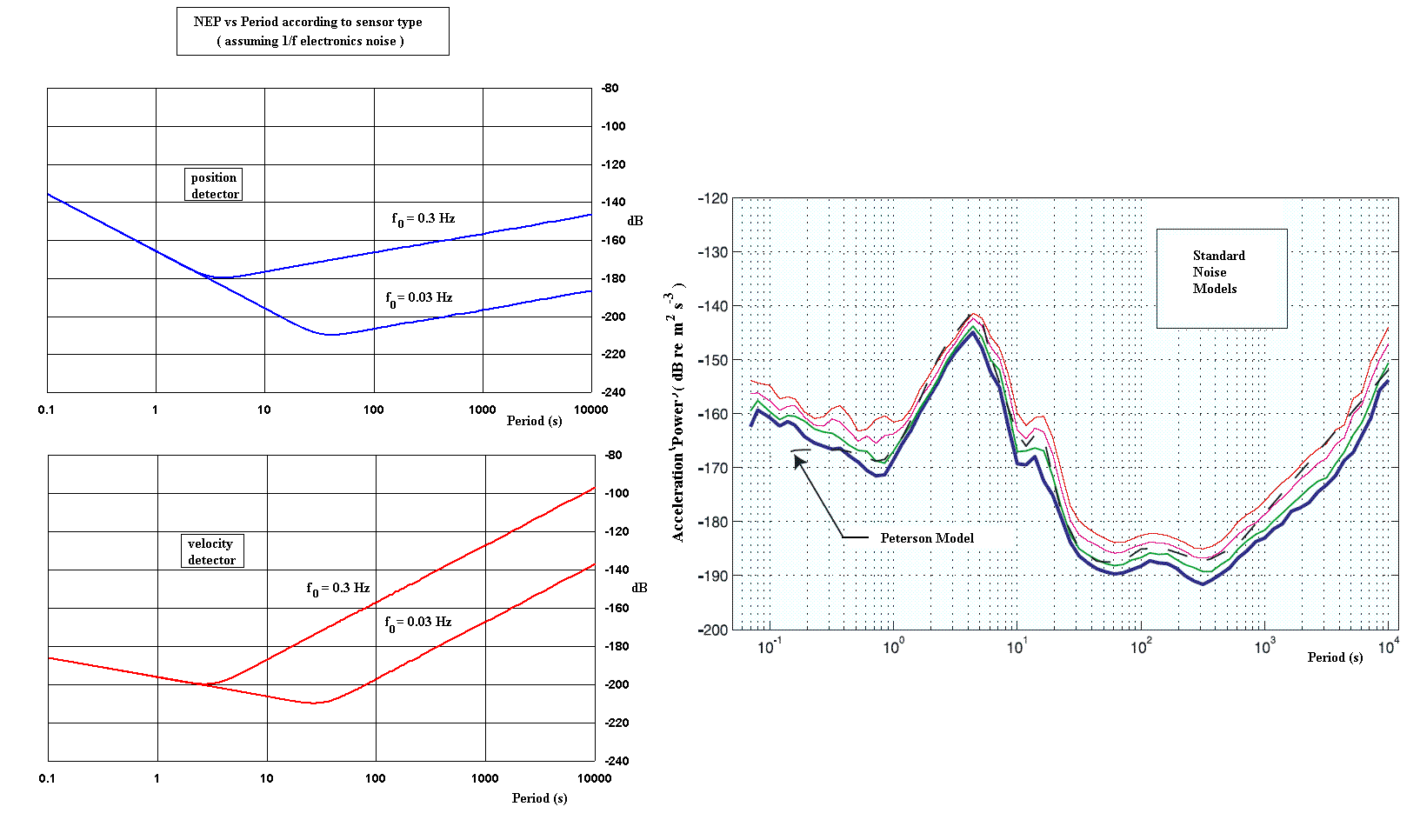
Figure 2. Examples of theory-estimated NEP (left pair of graphs) for
different sensor types, showing change that results by decreasing the natural
frequency from 0.3 Hz to 0.03 Hz. The right graph is a plot of Acceleration
``power'' (ascribed to earth noise) that is commonly used as a benchmark
for seismometer performance. Electronics matching has been effected for the
position and velocity cases at the 30 mHz corner frequency.
The first significant point to note from Fig. 2 is that lengthening the natural period from 3.33 s to 33.3 s decreases the NEP of each detector-type by 40 dB, for periods beyond approximately 33.3 s. This is expected because of the hundred-fold increase in sensitivity that results.
The lower left graph (30 mHz `corner frequency' case) in Fig. 2 is similar to commonly published earth noise `models'; i.e., the right graph of the figure. A careful tailoring of the frequency dependence of electronics noise could be used to effect a nearly perfect match (after removing the `hump' due to microseisms). This improves confidence in the assumptions used to develop the present model of NEP.
The author has arrived at two conclusions on the basis of this study: (i) not only can seismometers be expected to demonstrate significantly improved low-frequency performance by changing to position sensors, but also (ii) the noise that has been ascribed to the earth at low frequencies is at least partially an expression of instrument limitations due to the NEP being too large to allow good measurements.
There is another feature of the NEP that has not been considered, even though it is a linear effect--the influence of tilt. A later paper will address the `crossover' between horizontal acceleration and tilt that occurs for periods in the vicinity of 1000 s. Horizontal acceleration dominates the transfer function of a pendulum (for seismic waves) over nearly the full-range of periods shown in Fig. 2. Tilt becomes dominant, however, for periods greater than about 1000 s, where eigenmode oscillations are most important. The seismic community has failed to account for the importance of this effect, as it influences the NEP. The bending over of NEP at long periods because of tilt allows a pendulum to be a much more effective instrument for measuring earth oscillations than conventional wisdom has thought possible.