
Figure 1 Photographs of the modernized conventional pendulum.
The detector employed for decades by seismometers was a Faraday-law velocity sensor. As compared to a displacement sensor, its sensitivity falls off rapidly below the lower corner frequency of the electronics. Although most modern instruments use a capacitive displacement sensor, the style of force-feedback used with the sensor causes the system at low frequencies to be analogous to a Faraday-law detector. For study of the increasingly important mHz range (as well as lower frequency) motions of the Earth, velocity detection is seriously deficient. Oscilloscope users will recognize the source of the deficiency immediately; i.e., one cannot view low-frequency signals with the instrument when it is a.c., as opposed to d.c. coupled at the input.
Low-frequency instrument limitations have disallowed conventional seismometers from being an effective means to study the anelasticity (source of internal friction) that is present in their mechanical oscillatory parts. Conventional wisdom about damping and noise of these instruments is invalid at low energies, because of the nonlinear (complex) processes of mesoanelasticity. An instrument configured to amplify earth motions will also amplify the `noises' of its own dynamic structure. Just as the Earth is not a static body, but evolves in time, through chaotic processes due to anelasticity; so a seismometer is never static. Strain of materials, from which it is built, is not even continuous; it is instead `jumpy' because of the Portevin LeChatelier effect. Structural evolution never stops completely, because there is no level below which creep is no longer measureable with modern sensors.
An approach showing promise toward overcoming some of these difficulties is the following. Sensor technology, and understanding of the electronics whereby various detectors operate, has advanced much beyond our understanding of the internal friction of materials [1]. Thus, in the compromise between `mechanical amplification' versus `electronic amplification'; a greater emphasis should be placed on the latter. This was unnecessary when sensors were primitive, and attention was focused on higher frequencies associated with the p and s waves of earthquakes. It is no longer true as interest increases in the low-frequencies of free-earth oscillations.

Figure 1 Photographs of the modernized conventional pendulum.
External damping is not used with this instrument, since it was designed for monitoring frequencies well below resonance. Shown in Fig. 2 is a free-decay record that illustrates (i) its low damping, with a Q of 290, and (ii) the electronics threshold determined by the Dataq adc (DI-700).
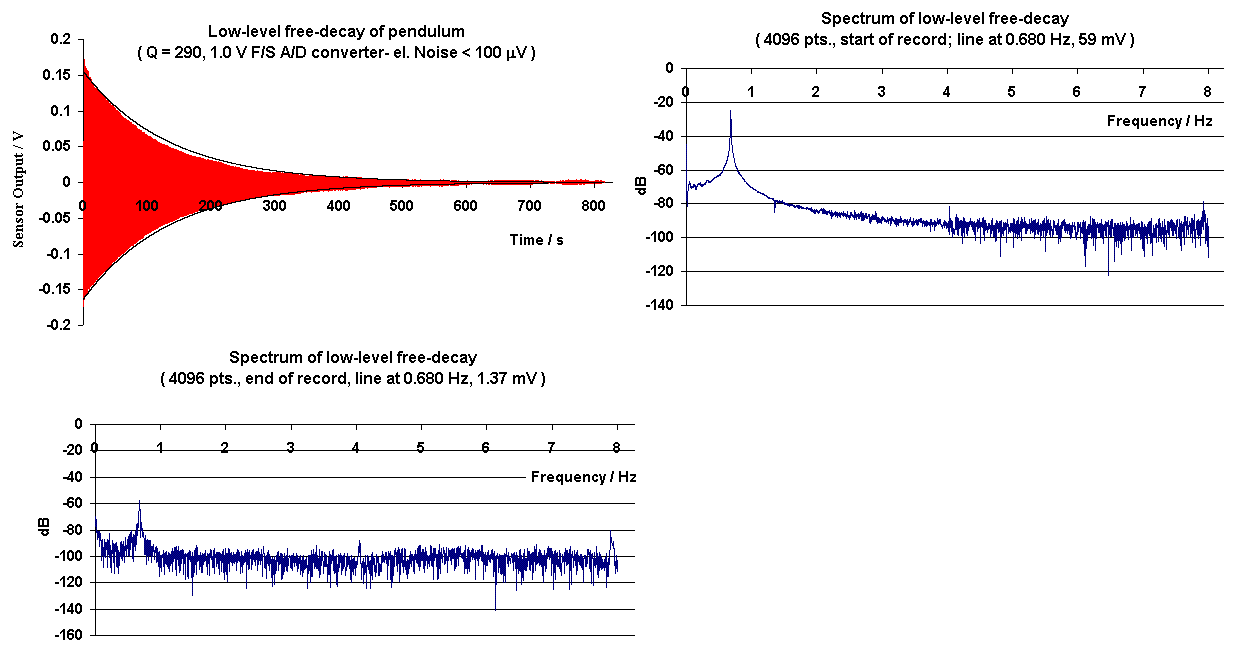
Figure 2. Example of pendulum sensor output for a free-decay.
The instrument was not designed to detect earthquakes, yet figure 3 shows that it responds well to larger and/or closer disturbances.
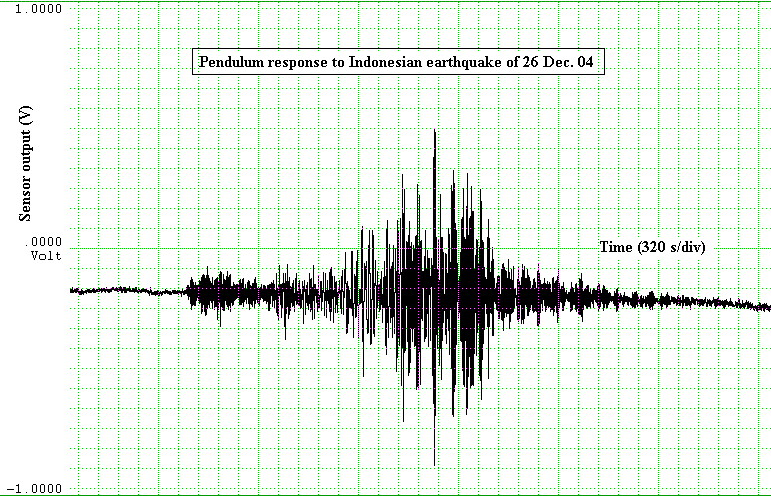
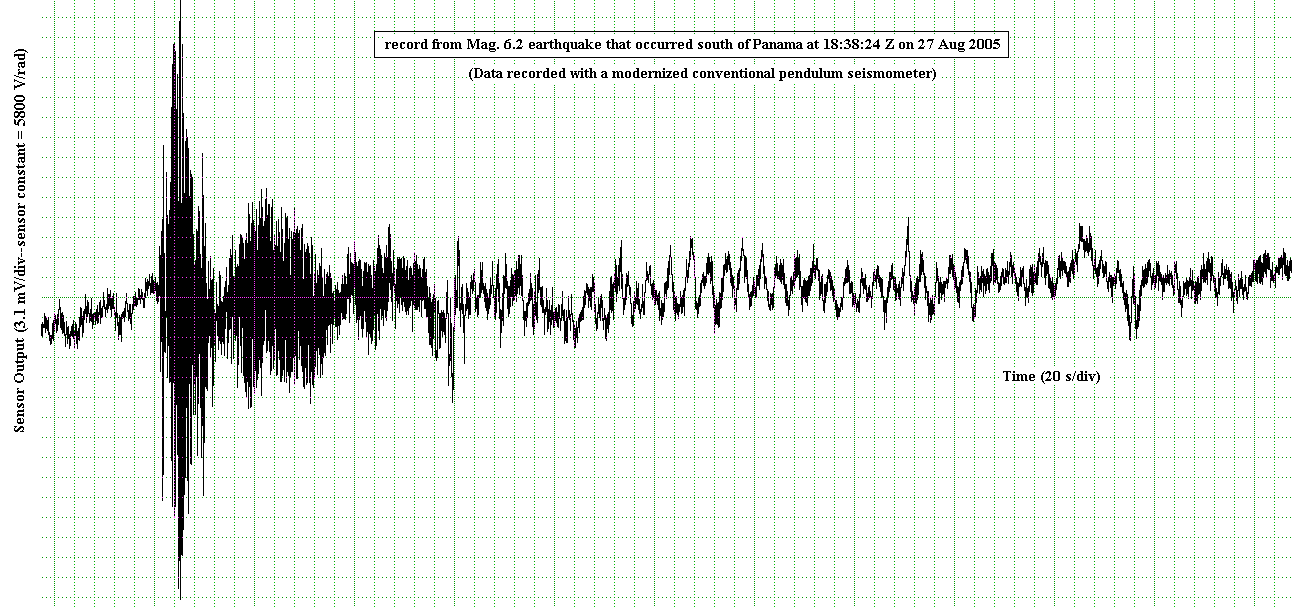
Figure 3. Examples of earthquake records with some similarity
to the output from other seismometers.
In both of the cases shown the p and s waves cause a very large response at the pendulum's eigenfrequency of about 0.7 Hz, which disallows use of the instrument for many conventional purposes (unless one were to remove the instrument response by means of post-processor deconvolution).
The low-frequency advantages of this pendulum are illustrated in Fig. 4, which shows: a precursor to the second of the earthquakes illustrated in Fig. 3, and also the presence of an Earth-mode during this same earthquake. It is likely that these unusual modes were made more readily observable because hurricane Katrina was very energetic over the Gulf of Mexico on 27 Aug. 05.
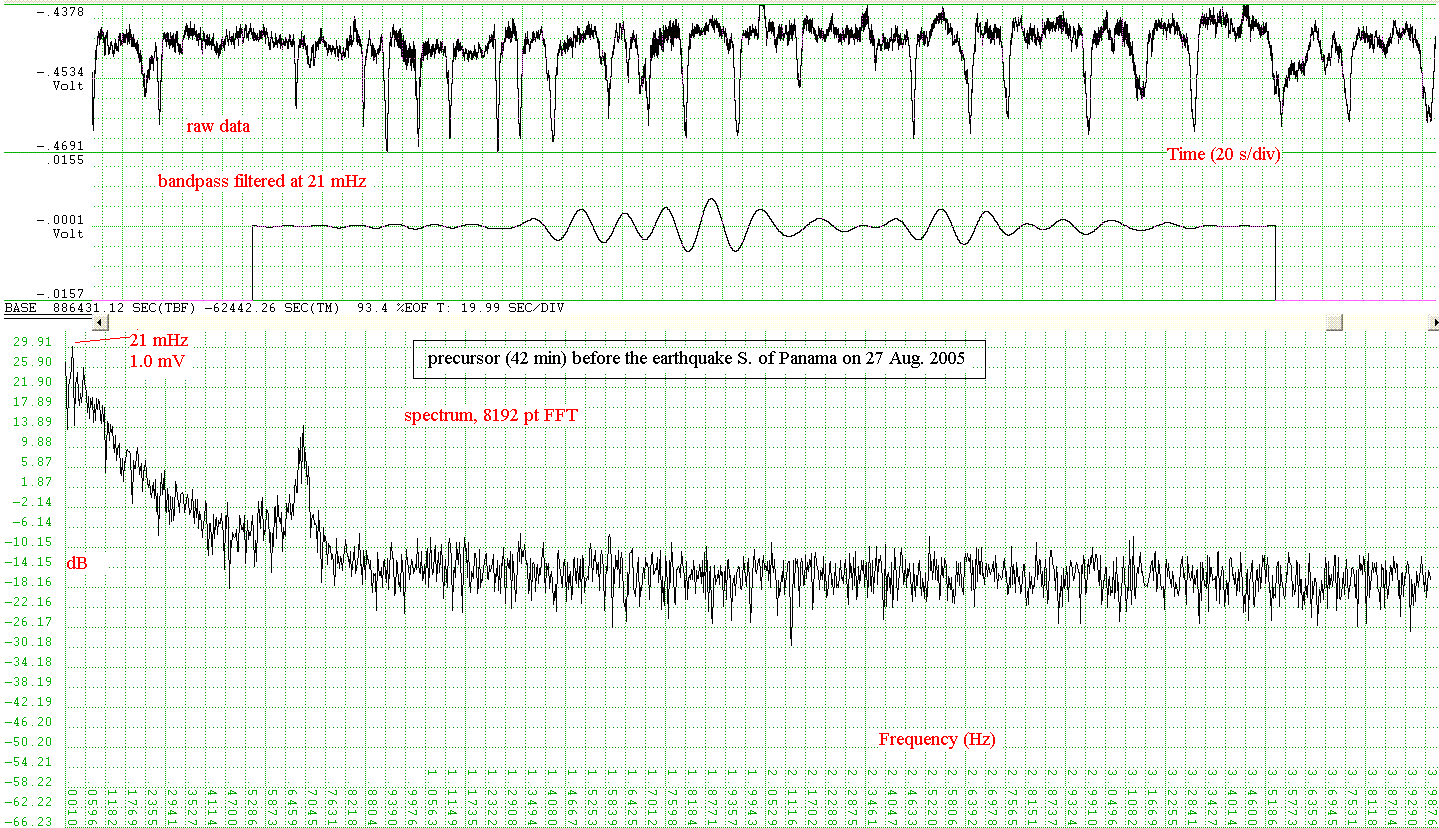
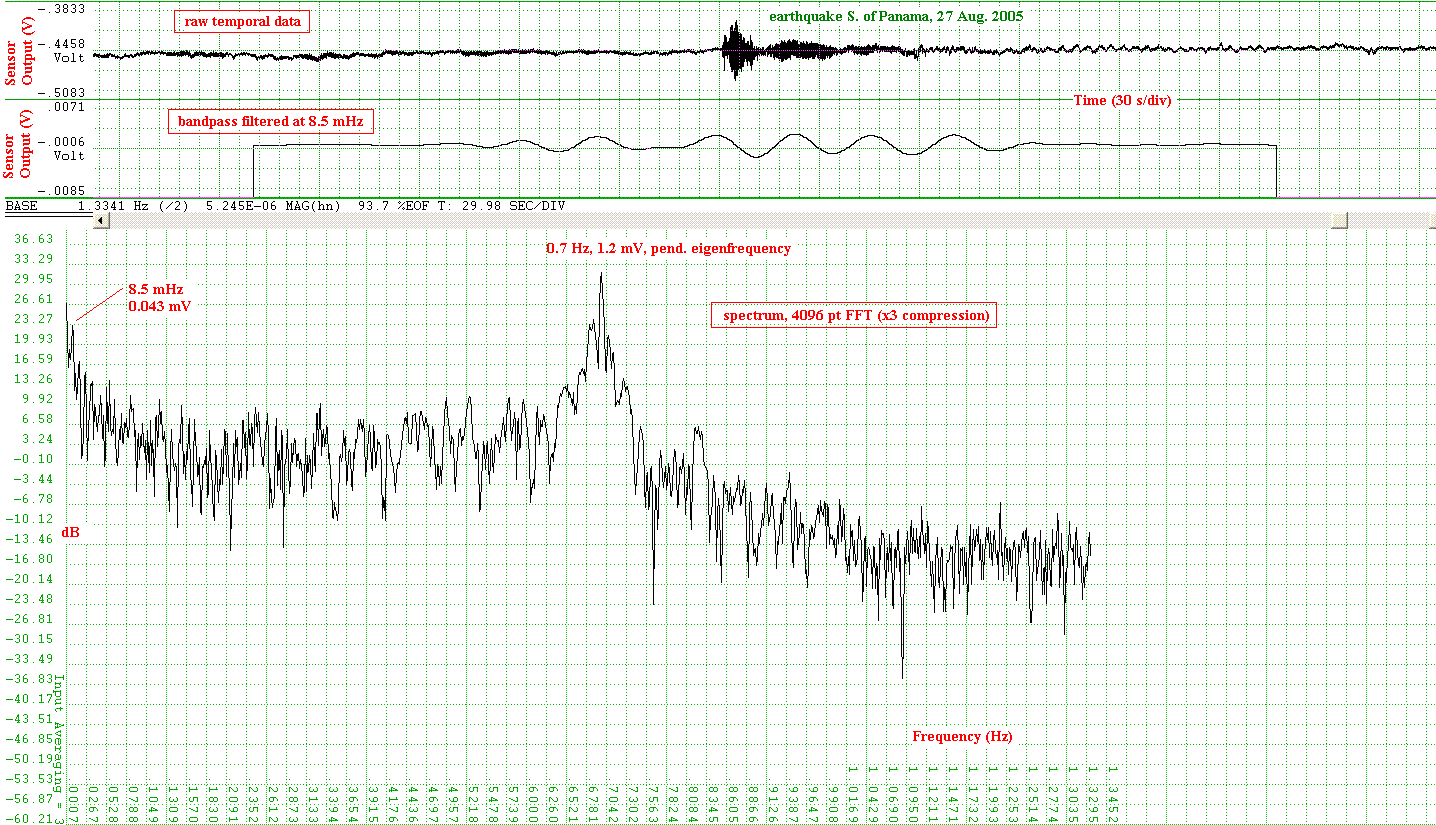
Figure 4. Short-lived coherent low-frequency oscillations
observed with the
pendulum, and associated with the earthquake south of Panama on 27 Aug. 05.
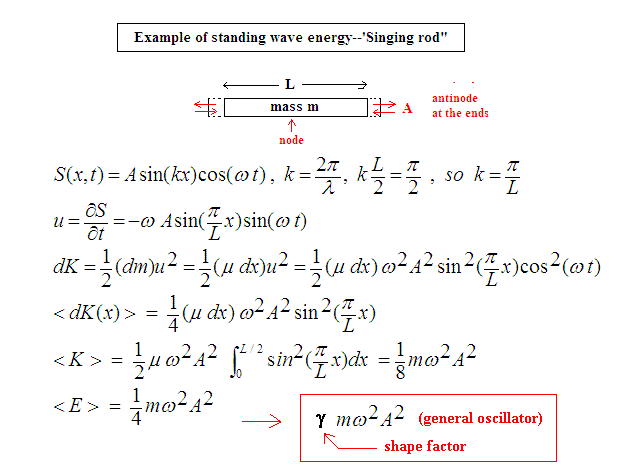
Observe that the energy depends on the total mass of the rod m, the square of the frequency f (where w = 2pf), and the square of the amplitude A of oscillation. A precise extrapolation of this case to that of Earth oscillations is not trivial, since the standing waves are three dimensional instead of one-dimensional; and the mathematics involves spherical harmonics instead of a simple sine function. Nevertheless, the shape factor g (for a general oscillator including the Earth) is expected not to deviate from unity by more than an order of magnitude. The large mass of the earth (first measured by Henry Cavendish, approx. 6×1024 kg) requires large energy sources if any of the eigenmodes are to be excited above the noise level of a seismometer. It will be shown from energy estimates of some modes that were observed, that hurricanes and large earthquakes have plenty of energy to excite them.
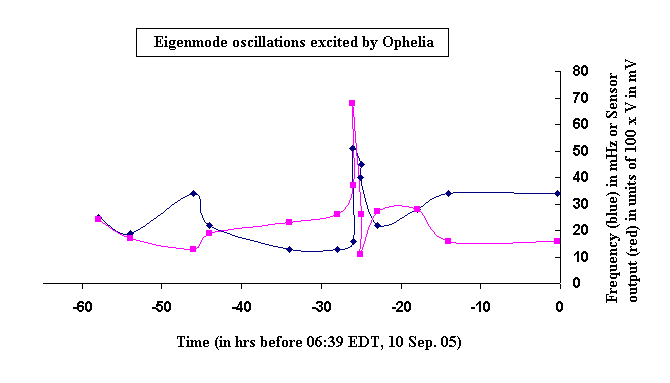
In the case of hurricane Ophelia, the eye of the storm was nearly stationary for more than two days off the coast of Florida near Cape Canaveral. During this stationary period, the eye was located very close to the edge of the contintental shelf. In straddling the edge in this manner, the northerly component of the winds `stroked' the Florida peninsula through the shallow waters over which they were blowing (near the coast). The sourtherly component of the winds, further out in the Atlantic, were blowing over much deeper water. The conditions were ideal for friction-generated oscillations.
Shown in Fig. 6 is the largest of fourteen modes that were observed in
the three-day period devoted to the study of Ophelia. The mode that
is shown
occurred when the microseisms that
were continually present during this three-day period were at their
maximum intensity.
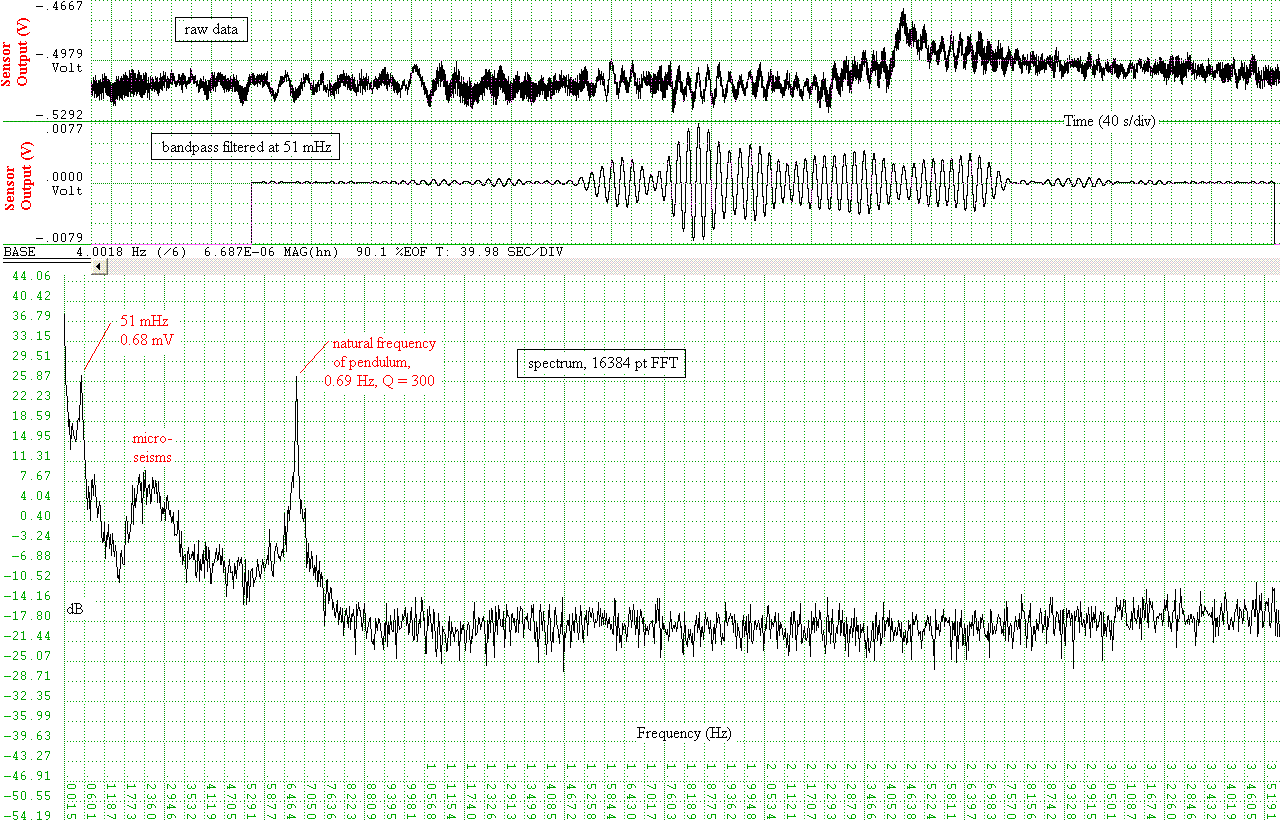
Figure 6. Characteristics of a large eigenmode oscillation
as Ophelia was leaving its stationary position
off the coast of Florida.
It should be noted that the lifetime of modes presented in this and other studies by the author are much shorter than the free oscillations seen after huge earthquakes, such as that of Mag 9.2 on 26 Dec., 2004. The present modes are more like the low-level phonon modes of solid state physics, which according to the Debye theory, determine the specific heat of a material. Just as phonon-phonon interactions disallow long lifetimes in cm-sized samples, so the oscillations of the Earth being described here do not usually persist beyond about ten cycles. This is quite in contrast to some of the oscillations that were observed following the huge Indonesian earthquake of 2004. The Earth `rang like a bell' for days after that event, and individual spectral lines persisted for times that are much greater than the present case.
Ocean currents are known to be a primary factor in the thermodynamics of our planet, but body dynamics must also be important. After all, as noted in the previous discussion of the Debye model, the oscillations called phonons of a solid are what determine its temperature. Although the vast majority of similar oscillations in the Earth are at much greater (even incrediby higher) frequencies, the `phonon-equivalent' spectra of the Earth must include modes such as the ones being presently described. Support for the importance of these low frequency modes, relative to energy redistribution within the Earth, is provided by the following observation.
The weakening of the storm, mentioned in the caption of Fig. 7, is
described in advisory #12 from the National Hurricane Center
(05 AM EDT, 9 Sep 05). In a three hour interval, coincident with this
reduction in power output from the storm, five eigenmodes were observed;
even though the average excitation rate for the entire three-day period
was only 0.2 per hour. The swarm of modes was found also to coincide
with the maximum in the graph of microseismic intensity, shown in
Fig. 8.
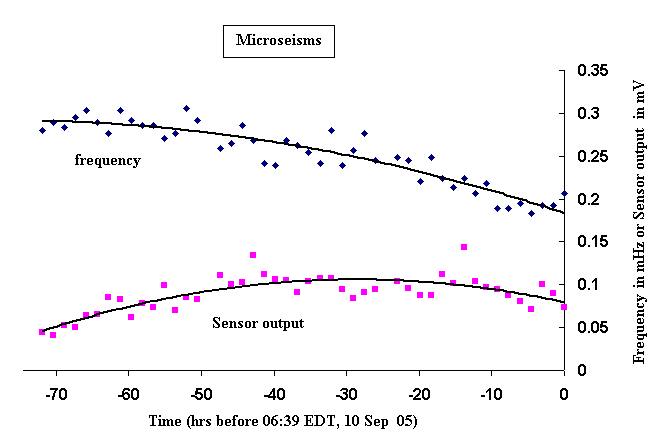
Figure 8. Spectral data of microseisms during cyclone Ophelia.
The single point that was selected from a given FFT, to
produce a datum in Fig 8, was the
spectral component with the
largest intensity within the `microseismic-hump' located
between 0.2 Hz and 0.3 Hz.
The prevailing theory of microseisms is based on the coupling of
wave motion to the ocean floor through the conversion of water
wave-induced pressure variations to seismic energy[7].
This author has been unable to find any mention
of earth modes in the theoretical
discussions. Yet the seismic energy must get distributed according to
the density of available states; which is determined by the geometry
of the Earth, both global and local. The breadth of the virtually
continuous microseismic
spectral `hump'is
suggestive of the excitation of numerous high frequency eigenmodes of the
Earth. At a typical peak frequency of 0.25 Hz, the density of modes of
an idealized spherical earth is
enormous, essentially a continuum. Occasionally, however, a sharp
spectral line emerges from the hump, as illustrated in Fig. 9.
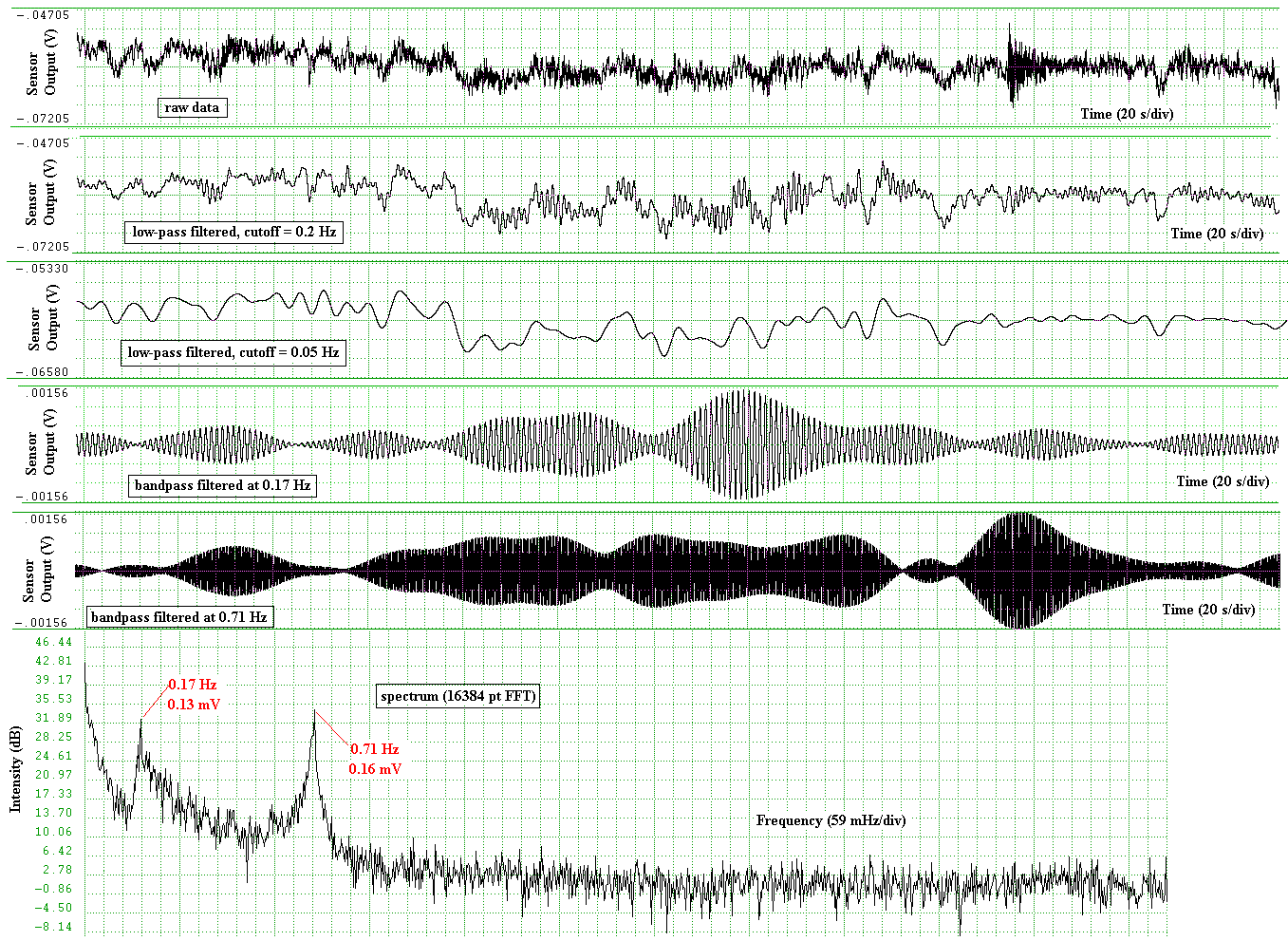
Figure 9. Sharp-spectral line in the background of
generic microseisms,
seven hours before the eye of hurricane Katrina crossed the Gulf coast.
Insofar as post-processor software is concerned; prevailing literature suggests that many of the algorithms being employed are antiquated and virtually useless as compared to codes that are now available. This probably explains why there are so many examples of microseism time plots, yet a paucity of spectral plots.
To extract meaningful spectral information from geophysical data generally requires the ability to easily position a time window of any size, anywhere within a record-subject to constraints of the data set. Only then can one identify the transient spectral features suggestive of physical mechanisms.
Adjustments of compression type must not `throw away data' (reminiscent of velocity detection), but instead average over subset values lest there be loss of information that is otherwise available. It is not enough to just generate any power spectrum. The ability to easily do various post-processor filtering operations, such as the examples shown in Fig. 9, is invaluable. Although one can in principle accomplish all of these operations with a spreadsheet [8], such methods are much too slow and cumbersome. Nevertheless, such exercises are extremely beneficial for appreciating the ideosynchrasies and power of the FFT[9], where the number of sampled points must be 2n where n is an integer.
Fortunately, some engineers have already provided an entry-level candidate for the third component of the triad mentioned above (software). The code that comes with all of Dataq's adc's (including their $25 10-bit pedagogical instrument) does everything mentioned above. All spectra presented in this article were generated with the Dataq code.
The most serious limitation is that the Dataq code cannot presently accommodate the word-bit size of 24-bit interfaces. The highest resolution of any of their instruments is based on 16-bit architecture. Additionally, the algorithms are constrained to operate only on data structured in their *.wdq format.
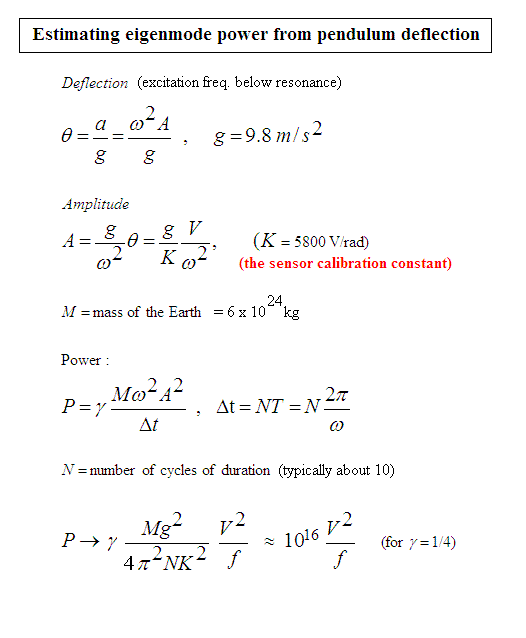
Figure 10. Assumptions used in the development of an
equation to approximately estimate the power
dissipated by an eigenmode oscillation of frequency f, having
spectral `intensity' V.
One of the beauties of the simple pendulum is evident within the derivation shown in Fig. 10; i.e., the ease with which the instrument is calibrated. The calibration constant of 5800 V/rad was measured by shining the beam from a He-Ne laser onto the mirror pictured in Fig. 1.
Shown in Fig. 11 is a graph of the estimated powers for each of
the 14 modes plotted in Fig. 7.
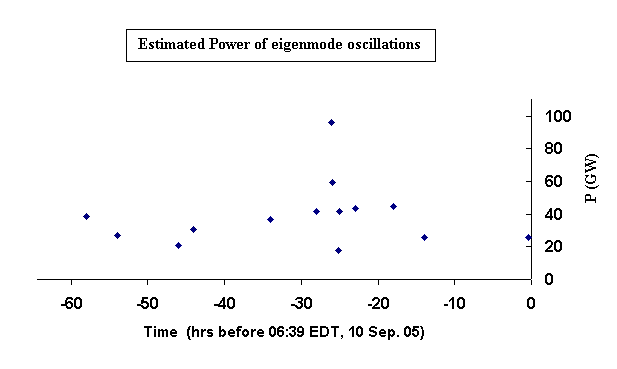
Figure 11. Estimated energy dissipation rates in GigaWatts for the
fourteen eigenmode oscillations plotted in Fig. 7.
Although these numbers might seem large, remember the earlier stated value for the power dissipated through friction by the winds of an average hurricane at the ocean surface; i.e., 1012 W.