Intuitive derivation of Reynolds number
Randall D. Peters1 and Loren Sumner2
1Physics and 2Mechanical Engineering
Departments
Mercer University
1400 Coleman Ave., Macon, Georgia USA
Introduction
In his article [1] titled, ``Life at Low Reynolds number'', Harvard Prof. Purcell says the
following: "...I'm going to talk about a world which, as physicists, we almost never think about.
The physicist hears about viscosity in high school ....and he never hears about it again ... And
Reynolds number, of course, is something for the engineers. And the low Reynolds number
regime, most engineers aren't even interested in...''
Dr. Purcell goes on to describe a world of small object dynamics that is alien to our
intuition; because at low Reynolds number, inertia is not important. This is a world with which
we should be increasingly concerned; since, for example, much of modern biophysics is
difficult to comprehend without an intuitive appreciation of the Reynolds number.
Being dimensionless, the Reynolds number (Re) is a natural parameter when it comes
to the Navier-Stokes equations. When Re is small, the flow is laminar. When Re is very large,
the flow becomes turbulent (chaotic). Thus the magnitude of Re is foundational to predicting
drag forces. For really small (low) values of the Reynolds number, the focus of Purcell's article;
the only force of importance is that which derives from the ``internal friction of fluids'' [2].
Interestingly, what Sir Stokes called the ``index of friction'' has come to be known as the
coefficient of viscosity.
It is evident from the literature that many engineers describe the Reynolds number
qualitatively as ``the ratio of inertial forces to viscous forces''. Yet it is not immediately
obvious that the well known expression Re = LVr/h, which involves the size L of a solid object
moving with speed V relative to a fluid of density r and viscosity h--is in fact a ratio of forces.
It is hoped that the following treatment, which is based on an energy rather than force
perspective, will help to de-mystify the important parameter given to us by Osborne
Reynolds [3].
Derivation
(Note: The following is not a rigorous derivation of Reynolds number, for that would defeat the
purpose for the paper.)
When an object is placed in an initially uniform flow, a portion of the fluid (approximate
volume L3) is forced to redirect around the object, causing the flow to accelerate upstream and
decelerate downstream. The viscous shear stresses do positive work on the object over an
effective area of approximate size L2. Reynolds number can be thought of as a comparison
between the relative magnitudes of two energy transfer rates. The time rate of change of the
fluid's kinetic energy is given by
![]() (1)
(1)
where V is the speed before alteration and dv/ds corresponds to acceleration along a flow line.
The power dissipated at the surface by viscous shear is given by
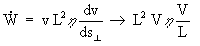 (2)
(2)
where it is assumed (consistent with the scaling) that the gradient of the velocity, perpendicular to
the flowlines, is comparable in magnitude to the acceleration along the direction of flow. Reynolds
number is obtained by dividing Eq. (1) by Eq. (2) to yield
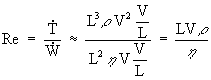 (3)
(3)
From these considerations, it is also possible to understand the Reynolds number according
to the qualitative 'engineering' terminology mentioned above; since Eq. (3) is equivalent to
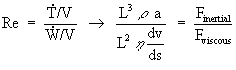 (4)
(4)
Acknowledgments: The authors are grateful to Dr. Peter W. Milonni of Los Alamos
National Laboratory for his influence in the development of this note.
References
1. E. M. Purcell, ``Life at Low Reynolds number'', Amer. J. Phys. Vol. 45,
3-11 (1977).
2. Sir George Gabriel Stokes, ``On the effect of the internal friction of
fluids on the motion of
pendulums'', Trans. of the Cambridge Phil. Soc. Vol. IX (1850). On the web at
http://www.ubr.com/ftp/stokes1850.pdf
3. Osborne Reynolds, Paper 44, "An experimental investigation of the
circumstances which
determine whether the motion of water shall be direct or sinuous, and of the law of resistance
in parallel channels'. Royal Society, Phil. Trans., pp. 52-105 (1883).