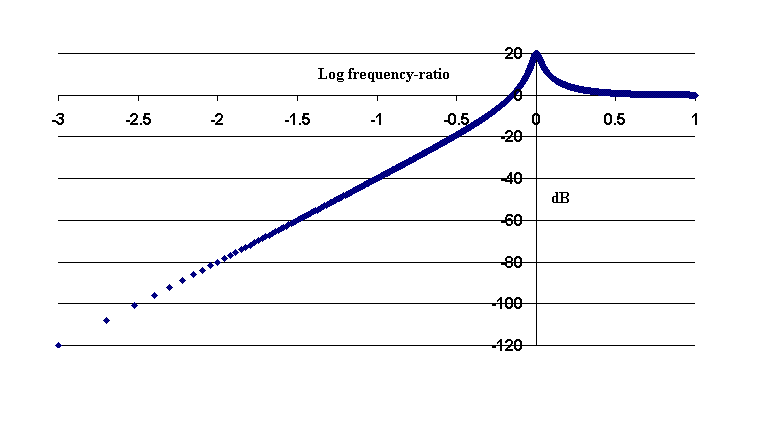
Figure 1. Graph of the ratio of steady state oscillator amplitude to drive amplitude as a function of drive frequency-ratio r, where r = w/w0. The graph was generated with Q = 10.
Randall D. Peters
Physics Department
Mercer University
Macon, Georgia 31207
(Copyright August 2005)
| (1) |
Here we assume a harmonic drive ad(t) = -w2 Ad ejwt where w is the frequency of the drive having amplitude Ad and j = (-1)1/2. Using the Steinmetz phasor method, one obtains the steady state solution to this well known equation. The result is frequently provided in terms of the Bode plot shown in fig. 1.

Figure 1. Graph of the ratio of steady state oscillator amplitude to
drive amplitude as a function of drive frequency-ratio r, where
r = w/w0. The graph was generated with Q = 10.
The equation used to generate Fig. 1 is
| (2) |
| (3) |
The secondary creep/creep recovery rate is assumed to be proportional to the acceleration; i.e.,
| (4) |
| (5) |
Substituting Eq.(5) into Eq.(3) and solving for the steady state solution with creep, yields an expression involving the sum of two terms. The first term of the new solution yields a Bode plot identical to Fig. 1, and the second term of the new solution yields the Bode plot shown in Fig. 2.
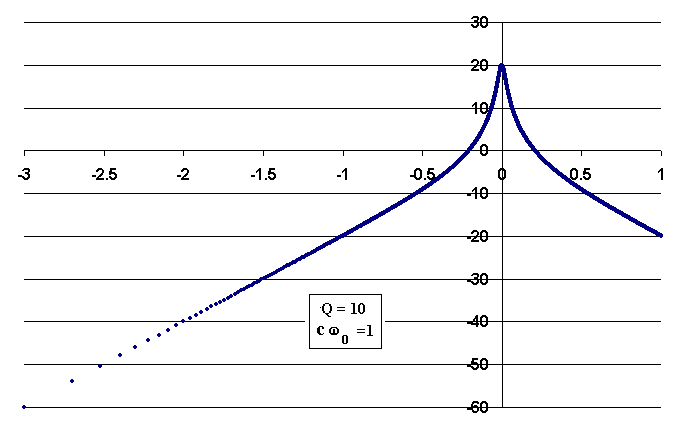
Figure 2. Normalized Bode plot for the creep component of
the new solution.
The complete response is obtained by adding c w0 times Fig. 2 to Fig. 1.
The equation used to generate Fig. 2 is
| (6) |
The difference in shape of figures 1 and 2 gives rise to practical consequences. When driving at frequencies above, or in the vicinity of resonance (r = 1), creep is inconsequential. For frequencies below resonance, creep can yield an increased amplitude response. Observe that in this regime, the fall-off of Fig. 1 is 40 dB/decade, whereas that of Fig. 2 is only 20 dB/decade. If the constant c is not vanishingly small, then the creep could allow signals to be detected at low frequencies, that would otherwise be below noise.
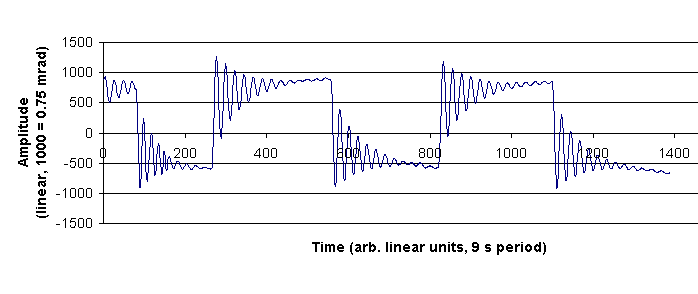
Figure 3. Illustration of creep in an unconventional torsion pendulum.
The instrument in this case was a torsion-gravity pendulum acting as a tiltmeter (remotely similar to a `garden gate' horizontal seismometer). Because the tungsten torsion wire of the pendulum is tied to both the top and bottom of the case, the instrument is tilt sensitive. For that reason the mean position could be easily adjusted using a piezo-translator, since the restoration depends on the Earth's gravitational field as well as the shear modulus of the wire.
It is seen that changes of only a few hundred micro-radians are accompanied by a significant creep response-for the ratio of drive frequency to natural frequency in the vicinity of 0.04. Clearly the creep coefficient of Eq.(5) is for this case too large to be ignored for its influence on the instrument's response at low frequencies.