Compound Pendulum to Monitor Hurricanes and

Compound Pendulum to Monitor Hurricanes and Compound Pendulum to Monitor Hurricanes and Tropical Storms

Randall D. Peters
Physics Department
Mercer University
Macon, Georgia 31207

(Copyright October 2006)

Abstract

The period of an undamped compound pendulum has been selected to maximize the instrument's response to microseisms, when functioning as a type of horizontal seismometer. When functioning as a tiltmeter, the instrument is also capable of monitoring eigenmode oscillations of the Earth. Other instruments designed by the author, some of which were monitored during hurricanes, suggest that storm seismicity in the frequency range of this pendulum could aid the process of hurricane forecasting.

1 Background

All conventional seismometers operate with damping that is close to critical. The transient response that would otherwise be present is unacceptable for monitoring anything of earthquake type other than the long-period seismic waves associated with teleseismic events.

For microseisms there is not a similarly great need to easily time-resolve specific attributes such as the arrival time of p and s waves used to determine distance of an earthquake from the sensor. Because the primary microseisms are localized in frequency in the vicinity of 0.25 Hz, it is therefore meaningful to take advantage of the response magnification of an undamped pendulum with reasonably high Q.

2 The Pendulum

Shown in Fig. 1 is a photograph of the instrument, illustrating its mechanical geometry. Holding the various parts `rigidly' together is a high tensile strenth 1/4 in aluminum alloy rod. The pendulum uses two disc shaped lead `bobs' of approximately 5/8 in thickness and diameter 2 in. The lower bob is rigidly fixed to the rod and the position of the upper bob is adjustable by means of the thumbscrew which seats against the rod via a threaded hole that was tapped in the lead. On the oppose side of the thumbscrew a large nut is visible in the picture; its placement on the horizontal aluminum tube determines the equilibrium position of the pendulum.

Figure 1. Photograph of the compound pendulum having a period of 4 s. The natural frequency of the undamped instrument is thus a reasonably close match to the peak frequency of primary microseisms.

The axis of the pendulum is a pair of small tungsten carbide balls (taken from writing pens) resting on sapphire plates. Grounding of the rod, the bottom of which holds the moving electrode of the capacitive sensor, is accomplished by means of a long, coiled, small diameter copper wire.

The position sensor is a four-element array-form of the symmetric differential capacitive sensor patented by the author. It is one form of the first fully-differential capacitive detectors [1].

The instrument shown is of a type that has been extensively used by the author to research internal friction [2]. As the period is lengthened by raising the upper mass (and thus causing the center of mass to approach the axis), the sensitivity to high frequency disturbances decreases in accord with Fig. 2.

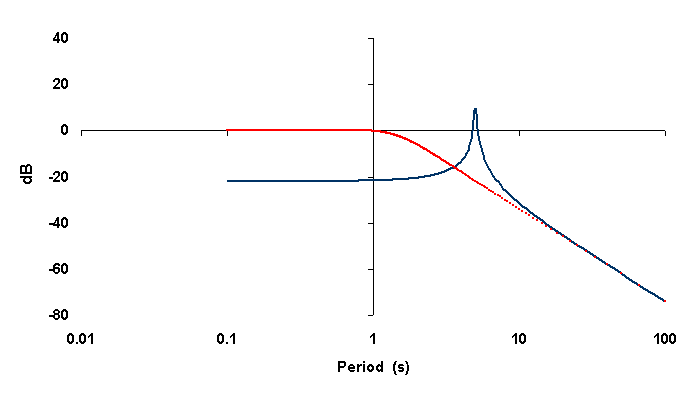
Figure 2. Bode plot showing response of the undamped compound pendulum (blue) with period 4 s, Q = 40, compared to a horizontal seismometer having a period of 1.1 s and Q = 0.8 (red).

The dB ordinate is defined as 20 times the log to the base 10 of the ratio of the steady state amplitude of the pendulum to the amplitude of earth harmonic motion. It is seen that only a modest Q = 40 raises the sensitivity of the instrument dramatically for purpose of observing microseisms. Coupled with this is a significant reduction in high frequency sensitivity, which is the dominant realm of local noise sources. Thus the instrument's signal to noise ratio for detecting primary microseisms of 4 s period is expected to be exceptional.

2.1 Tilt Response

The Bode plot of Fig. 2 describes only the response of the pendulum to horizontal acceleration. Any pendulum using a position sensor, as opposed to the velocity sensors used in conventional seismometers, responds also to low frequency tilt. Unlike the response shown in Fig. 2, the tilt response does not fall off for frequencies below the natural frequency of the instrument. Even ordinary pendulums thus constitute an important means for studying eigenmode oscillations of the Earth, sometimes referred to as Earth hum. Illustrated in Fig. 3 are several of the spherical harmonic modes to which the pendulum would respond if it were positioned anywhere along a nodal line, the numbers of which increase with order number.

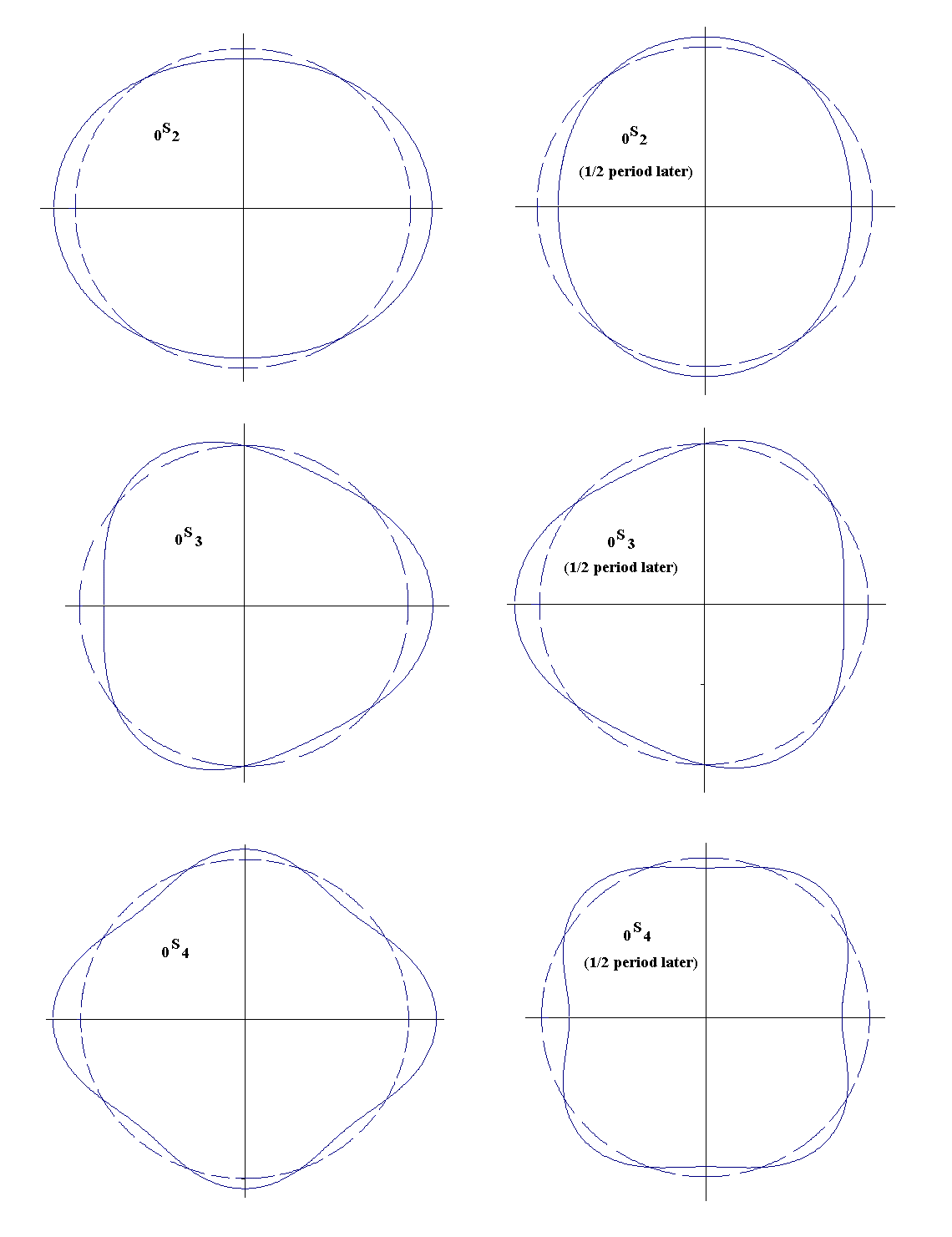
Figure 3. Illustration of eignemode oscillations of an assumed spherical earth corresponding to pure spherical harmonic modes.

To the present, only the author has exploited this powerful new means for studying our planet.

2.2 Convection

At low frequencies the pendulum is very sensitive to changes that occur in the instrument as opposed to earth generated disturbances. Complex processes associated with anelasticity require that the pendulum be given time following setup to stabilize against creep. Such changes are not necessarily smooth but can involve `snap, crackle, pops' of the Portevin LeChatelier effect [3]. Additionally, and one of the worst influences on low frequency performance if not eliminated, is that of Rayleigh Benard convection of the air surrounding the pendulum, inside the enclosure. The pendulum must be operated inside an enclosure to prevent air currents of the room from driving it to very large levels. Even so, the establishment of certain thermal gradients in the enclosure air can result in oscillations that persist for many minutes (or even hours), such as shown in Fig. 4.

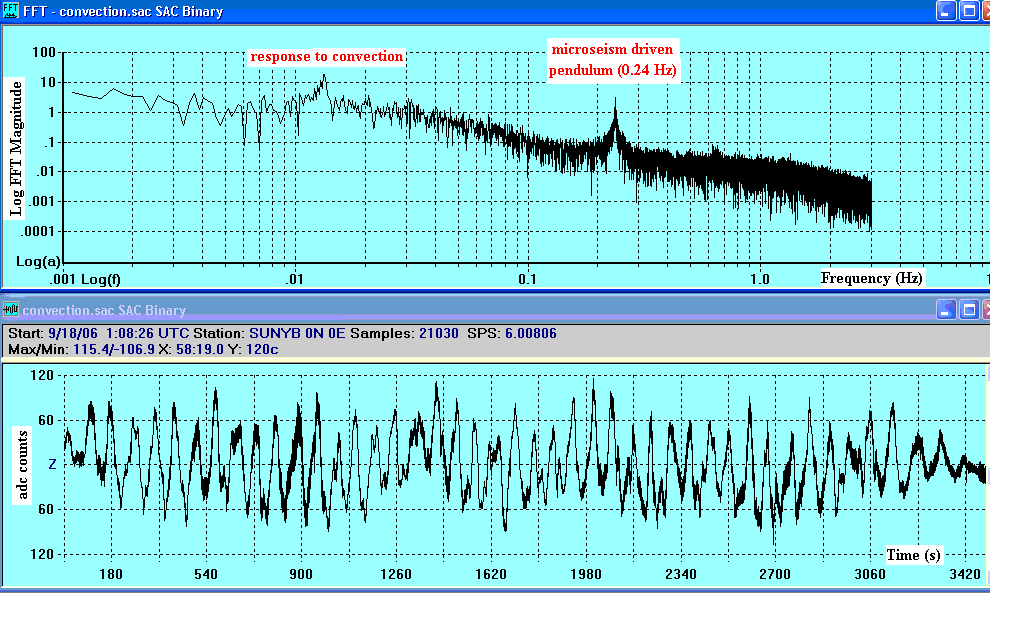
Figure 4. Example of troublesome convection response due to thermal gradients in the air of the enclosure.

The convection was eliminated by shining a light bulb on the top of the metal garbage can used as the top part of the two-part enclosure. The lower part is a cylindrical portion of a fixed nylon barrel; off which the can is easily removed/replaced for purpose of adjusting the pendulum.

3 Example Data

Shown in Fig. 5 is a record that was collected for an interval approaching 24 h. The spectrum has been scaled relative to the maximum component observed during this time (microseisms), and plotted on a linear rather than logarithmic scale. The linear scale shows more clearly the mHz structure associated with the pendulum's response to persistent eigenmode oscillations (earth hum). Based on data collected with other of the author's different instruments during hurricanes, the spectrum below 10 mHz is expected to become distinctly different and highly variable during powerful storms.

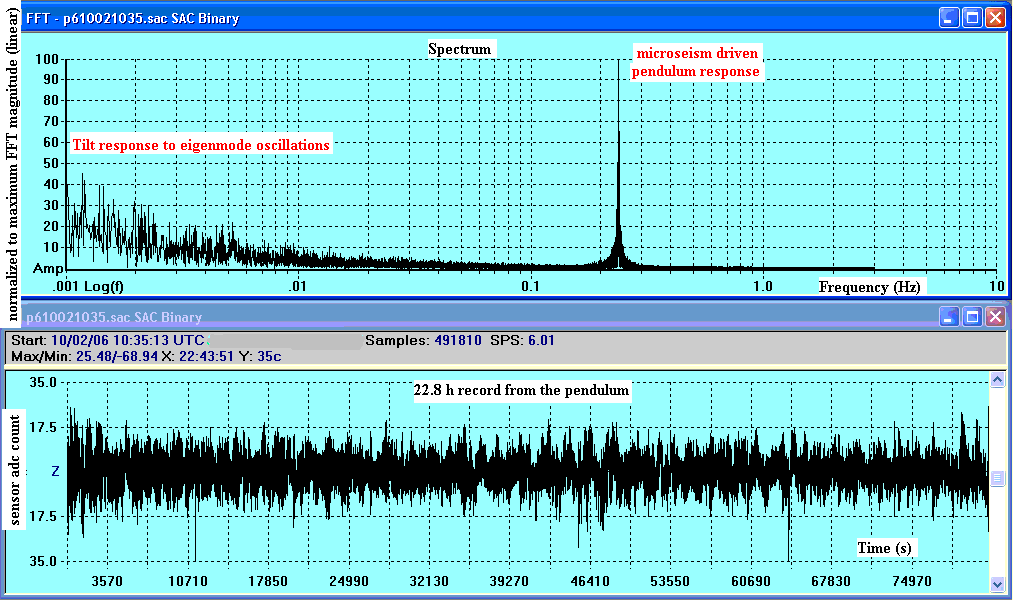
Figure 5. Example pendulum response showing both microseisms and eigenmode oscillations of the Earth.

Fig. 6 shows a portion of the Fig. 5 record in which the spectrum is plotted in the more common log-log form. The time plot shows clearly how the microseisms rise and fall in time, typically enduring for about 20 cycles.

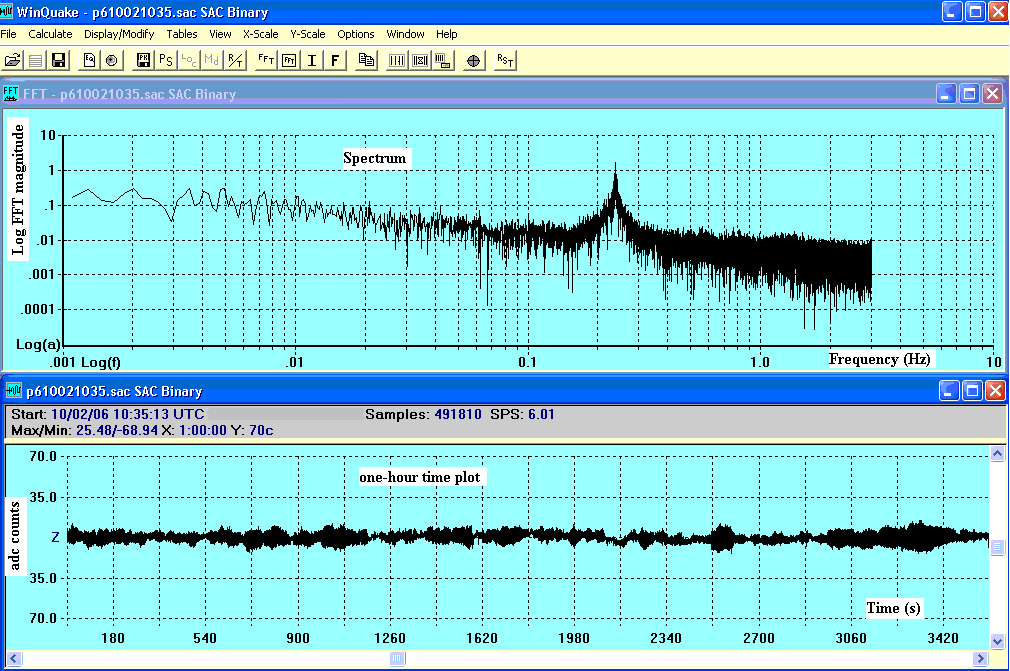
Figure 6. One-hour portion of the Fig. 5 record showing coherence length (`average' about 20 cycles) of the microseisms.

Figure 7 shows how microseismic activity declined noticeably during a one day interval from 23 September to 24 September 2006. For the plot shown, the record was sharply bandpass filtered around 0.24 Hz.

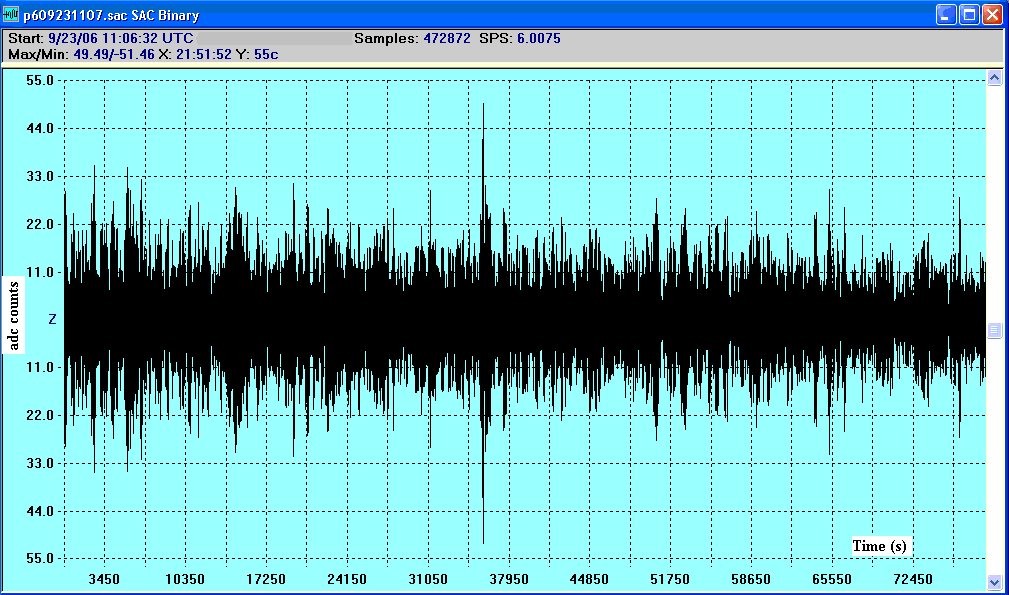
Figure 7. Temporal plot showing the decline in microseismic activity during a 22 h interval. It was at this time tropical storm Helene was losing its tropical characteristics in the vicinity of the Azores.

4 Acknowledgments

Mr. Jimmy Strates, high-school student from Orlando, Florida provided outstanding assistance in the building of this instrument during the summer of 2006. The software used to generate the figures was written by Larry Cochrane of Webtronics. Data collection was with a program (Amasend98) written by Kip Weiss of Symmetric Research, to feed the Amaseis program written by Alan Jones and distributed by IRIS.

Bibliography
(1) Symmetric differential capacitance transducer employing cross coupled conductive plates to form equipotential pairs, U.S. Patent No. 5,461,319. Online information provided at http://physics.mercer.edu/petepag/sens.htm
(2) R. Peters, Friction at the mesoscale, Contemporary Physics, Vol. 45, NO. 6, 475-490 (2004).
(3) R. Peters, ``The Pendulum in the 21st Century-Relic or Trendsetter'', pp. 19-35 in The Pendulum, Scientific, Historical, Philosophical & Educational Perspectives, ed. M. R. Matthews, C. F. Gauld, & A. Stinner, Springer 2005. Online paper at http://arxiv.org/html/physics/0207001

File translated from T_EX by T_TH, version 1.95.
On 11 Oct 2006, 14:42.