Precursor Warnings of Structural Catastrophe through

Precursor Warnings of Structural Catastrophe through Precursor Warnings of Structural Catastrophe through observation of a Seismic `Bounce'

Randall D. Peters
Physics Department, Mercer University
Macon, Georgia
Copyright August 2007

Abstract

Novel technology employing two synergetic tools, one hardware and the other software, provide clear evidence for the possibility of preventing fatalities due to the collapse of structures.

1 Background

1.1 Events

Two August 2007 disasters in the United States prompted the generation of this article; they were the collapse of (i) the Minneapolis interstate highway bridge, and (ii) the Utah coal mine.

1.2 Relevant Science

Plenty of scientific knowledge is poised to address the challenges of predicting catastrophes of mechanical type. The main problem with the relevant database is that useful information has been distributed piece-meal among several disjointed scientific specialties. For example, the Portevin Le Chatelier effect, which was discovered in the early 20th century by French physicists [1], is virtually unknown to the physics community, even though materials scientists and engineers have studied the PLC effect for decades. This effect is one in which the strain of an alloy does not change continuously as increasing stress is applied to the specimen; rather, the strain exhibits `jerky' behaviour because of discontinous (catastrophic) alterations of state. Similar jerky behavior is well known to (early generation) electrical engineers familiar with the Barkhausen effect of magnetic materials.

Catastrophe theory is relevant to the hypothesis here presented, as noted by the following quote from the abstract of reference [2]: ``...extra responses are called ``catastrophes.'' This kind of behavior is summarized by the phrase `` ...the straw that broke the camel's back.'' Situations in which a gradually increasing force leads to a gradually increasing response, followed by a sudden catastrophic jump to a qualitatively different state, are all too common. They are seen, for example, iin the collapse of a bridge, ....'' Unfortunately, the `catastrophe functions' used by mathematical physicists to describe changes that disobey the fundamental theorem of calculus are esoteric and understandable by only a select few.

One might expect seismologists to be the key-holders of instrumentation to provide a solution to the prediction conundrum, since precursor `bounces' are expected to dominate the signature of incipient failure. Unfortunately, as explained in the material that follows, conventional seismometers are not well suited to the detection of these events. Moreover, probably a majority of seismologists view the matter of earthquake prediction as hopelessly complex.

NOTE: The term `bounce' was used by Utah miners to describe tremors they felt during work-shift periods that preceded the 8 August collapse that trapped their coworkers. In the material that follows, other examples of ground `bounce' is provided. These cases involve ground accelerations of localized type, studied with unconventional tools invented by the author. These comprise: (i) a novel hardware approach to measuring the displacement of the mass of a seismometer and (ii) a new software tool of digital data processing type-the seismic Cumulative Spectral Power (CSP).

2 Hardware

Unconventional seismometers developed by the author in a period spanning more than a decade were made possible by his invention of the first fully differential capacitive sensor [3]. Similar hardware has already made a significant technological impact on the electronics world [4].

2.1 Analog instruments

The SDC sensors have been used in a variety of seismic instruments. For example, one of the most common of the commercial seismometers used in the WWSSN [5] of a past generation-was modified by replacing the original Faraday law (magnet/coil) detector with an SDC sensor. This modified Sprengnether vertical instrument was made to function according to a `soft-force-feedback', accomplished by means of a long-time-constant integrator (SDC output into an opamp) feeding the original magnet/coil subsystem now acting as an actuator instead of a sensor as orginally configured. This soft-force architecture differs radically from that of `force-balance' used in commercial instruments. For frequencies below the instrument's eigenfrequency (but larger than the reciprocal of the integrator's time constant of about 3000 s), the output from the instrument is proportional to ground acceleration; whereas the output from commercial instruments is proportional to the derivative of ground acceleration (the `jerk').

Insistance on the use of a `velocity' sensor (jerk case) as opposed to a displacement sensor (acceleration case), is responsible for a serious degredation in the low frequency signal to noise ratio. This is easily understood from a consideration of velocity being the derivative of displacement. The derivative `pulls-out' frequency as a multiplicative term through the chain-rule of calculus. As the frequency decreases toward zero in progressing toward the spectral region of importance to `bounce' dectection, the multiplier term causes the instrumental self noise (such as the part due to electronics) to become larger than the low frequency signal one wishes to observe. In the case of `step' changes or bistable `pulses' shown in the material that follows, the effect of differentiation is to cause these precursors to become less obvious and to be easily confused with electronics artifacts.

In addition to the modified Sprengnether, the author has performed numerous experiments with a novel tiltmeter [6]. It also uses SDC sensing in the form of an array for improved sensitivity.

2.2 Digital Instrument

Whereas the modified Sprengnether uses digital electronics involving synchronous detection, a commercial instrument developed by the author and two business partners is the first fully-digital seismograph. The sensor electronics of other commercial instruments remains analog, similar to that of the modified Sprengnether, except using only a singly-differential, as opposed to fully-differential capacitive sensor. The VolksMeter uses fully-digital electronics along with fully-differential capacitive sensing. The instrument was built around the award winning `capacitance to digital converter' integrated circuit developed by Analog Devices [8].

3 Examples

An example of seismic bounce (bistability) is illustrated in Fig. 1. The pulses seen in the trace resulted from instability of the soil supporting the pier on which the instrument was placed. This soil was not properly compacted when supplied as backfill to the region; and similar bounces of greater intensity and frequency were noted during jackhammer activity when workers replaced a nearby concrete sidewalk.

The pulses are easily observed in the output from the author's tiltmeter, because of the excellent low frequency capability of the instrument. Such pulses would be less obvious if the trace were generated from the derivative of rotor position.

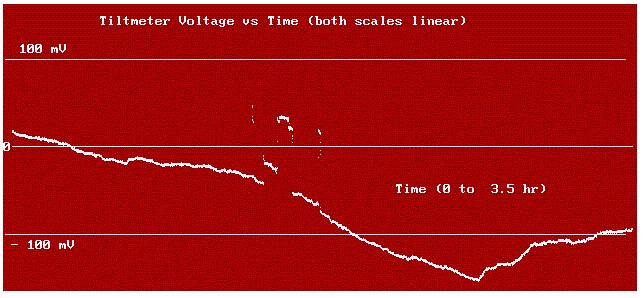
Figure 1. Pulses of bistability (`bounce') due to soil instability. The output voltage from the tiltmeter is proportional to rotor position. The record also shows features of diurnal secular change in mean position due to thermo-elasticity. Its influence can be removed by placing the instrument several meters underground.

At least some earthquakes are also preceded by seismic `bounces'. Evidence for this claim is provided in Figure 2.

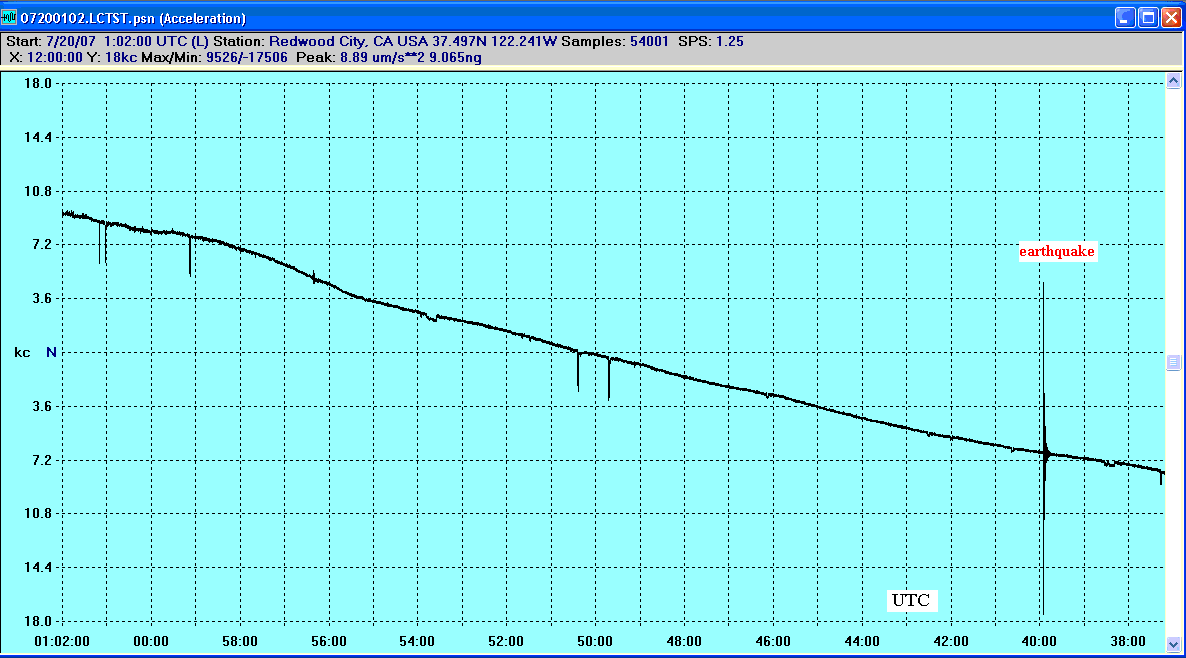
Figure 2. Pulses observed before the earthquake of 20 July 2007 near Oakland CA, by a VolksMeter seismograph situated in Redwood City, CA. In this 12-h total duration record, the first pulse occurs more than 10 hours before the Mw 4.2 earthquake.

The probability that pulses of this type can be seen is evidently determined by (i) magnitude of the earthquake, and (ii) its proximity to the seismometer (assuming the use of an instrement with d.c. capability).

Even close events are not readily detected by conventional sensing methods, as can be inferred from fig. 3.

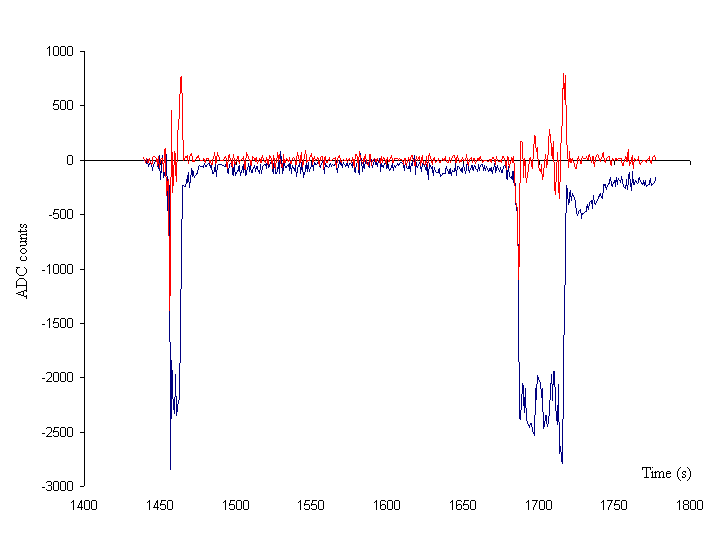
Figure 3. Close-up of a portion of Fig. 2 showing the first two pulses (blue, shown with an offset). The derivative of the record, generated numerically and shown in red, contains reduced information concerning the pulses while at the same time is more noisy.

The red curve is representative of what would have been observed with a conventional seismometer, as opposed to the VolksMeter. The pulse-edge `spikes' are much more likely to be interpreted as electronics artifacts.

4 Frequency Domain Analysis

For all of the preceding figures, the information presented is in the time domain. As is well known to the physics community, data from the frequency domain is frequently the more useful of the two. By this means, for example, seismologists concluded that the Utah mine disaster was not triggered by an earthquake. Rather, the spectral signature of the earth's vibrations measuring magnitude 4 on some nearby seismometers were consistent with a mine collapse independent of an earthquake.

The traditional tool with which to represent frequency domain data is either (i) the Fourier transform spectrum based on the FFT (Cooley Tukey algorithm), or (ii) the power spectral density (PSD). An FFT spectrum generated by two different seismometers will not be the same unless the instruments are identical, since the transfer function of an instrument (unique to that instrument) influences its output. Influence of the transfer function is removed during generation of the PSD; so it is superior, especially if one attempts to make absolute, as opposed to relative, sense of the data presented. Unfortunately, most spectra of PSD type generated by seismologists, appears to be limited to graphs used to evaluate instrument performance-as opposed to trying to analyze earth motions.

One of the difficulties with most real-world PSD's, as opposed to a case resulting from a highly monochromatic disturbance-is that they are inherently very noisy. The author has recently developed a means for dramatically reducing the spectral noise, by doing an integral over frequency of the PSD. The resulting curve is referred to as the Cumulative Spectral Power (CSP) [9]. The difference between the PSD and the CSP is similar to the difference between a probability density function and its cumulative probability equivalent. The cumulative function is obtained from the density function by integration (or conversely, the density is the derivative of the cumulative). Because integration is inherently a smoothing operation for random noise, the cumulative functions possess a significant advantage.

Shown in Fig. 4 is a series of both time records (upper graph-set) and their associated CSP's (lower graph-set). These correspond to 12-hour records collected not only on the day of the Oakland earthquake (red curve), but also (top graphs) each of the four days preceding that event. The start time per record was the same for each of the five days, and for the sake of clarity in the representation, the temporal plots (upper graph-set) have been shifted in mean postion from one another by 3000 adc counts.

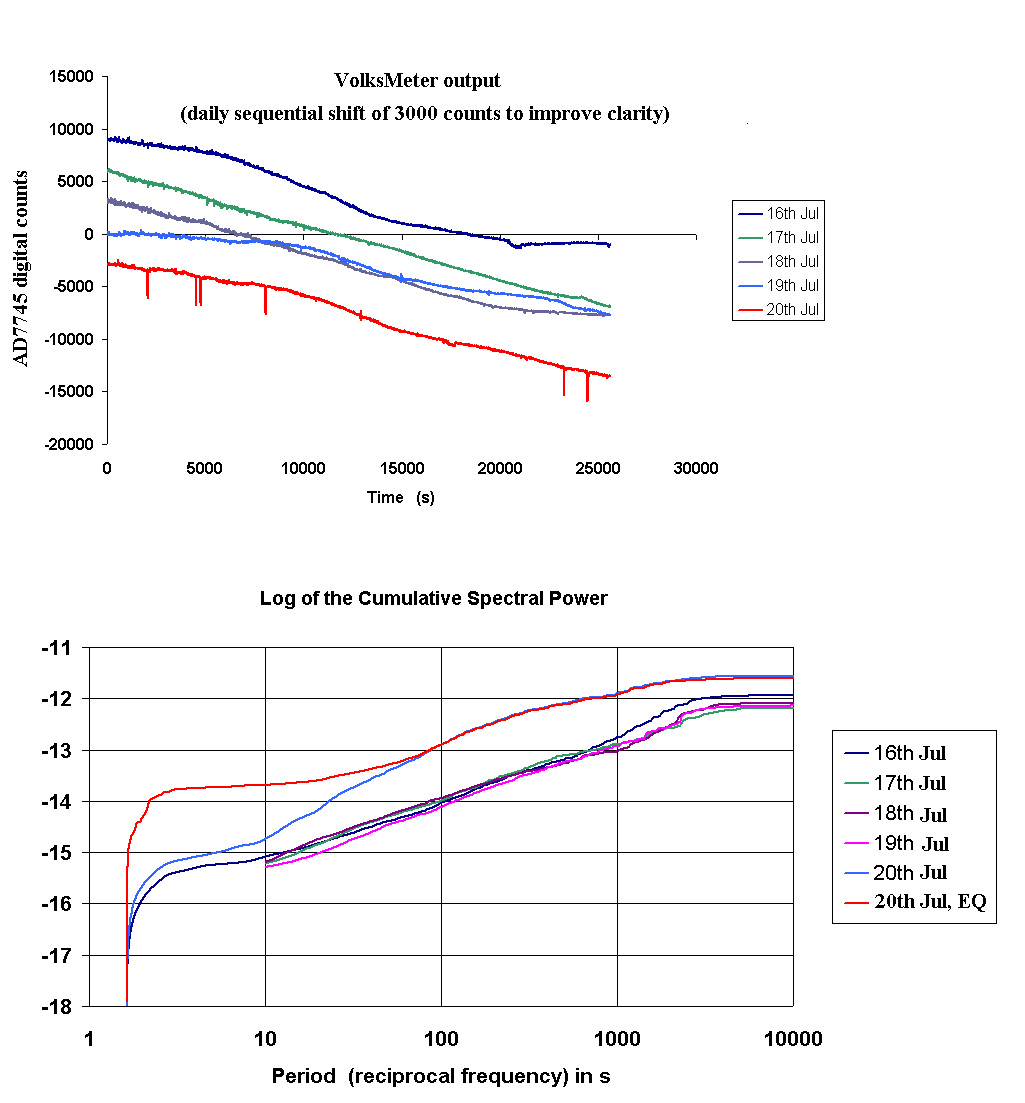
figure 4. Precursor information concerning the Oakland earthquake, presented in the time domain (upper graphs), and also the frequency domain (lower graphs) by means of the Cumulative Spectral Power.

The lower graph set shows six curves rather than five, to illustrate the energy buildup that occurred (blue curve, mainly at low frequencies) starting about 10 hours before the earthquake, due to pulse precursors. It is worth observing that the blue curve increases monotonically, which would not be the case for just any distribution-in-time of the half-dozen distinctly visible pulses in the upper graph red curve.

5 Conclusion

Suppose that hardware improvements of the type here mentioned have the potential to improve our knowledge of earth dynamics by two-fold. Further suppose that advantages of software improvement (CSP over PSD) constitute another two-fold increase. It is possible then, that the synergetic use of the two could amount to an order of magnitude improvement in predicting catastrophes in both the earth and in man-made structures. Only through testing with a significantly larger number of instruments can the hypothesis of this article be tested; i.e., that lives could be saved through observation of precursors to catastrophe.

Bibliography
[1] A. Portevin & M. Le Chatelier, 1923: ``Tensile tests of alloys undergoing transformation'', Comptes Rendus acad. Sci. 176, 507.
[2] R. Gilmore, ``Catastrophe theory: What it is-Why it exists-How it works'', AIP Conf. Proc-June 20, 1996-Vol 376, pp. 35-53, Intro. to chaos and the changing nature of science and medicine.
[3] Symmetric Differential Capacitance (SDC) Transducer employing cross coupled conductive plates to form equipotential pairs'', U.S. Patent 5,461,319 (1995). The SDC variant is related topologically to the first fully differential capacitive sensor, also invented by the author; i.e., ``Linear rotary differential capacitance transduer'', U.S. Patent 5,038,875.
[4] Jim Karki, ``Fully differential amplifiers'' Texas Instruments Application Note, Literature Number SLOA054B (2001)
[5] World wide standardized seismographic network. The Sprengnether instrument here mentioned uses a LaCoste spring, whose internal friction damping characteristics were first studied extensively by Gunar Streckeisen as a graduate student. Streckeisen is the builder of the `crown jewel' STS-1 seismograph, along with other STS instruments.
[6] Information on the tiltmeter is at www.iris.edu/stations/seisWorkshop04/PDF/NOVELTILTMETER.pdf
[7] A description of the VolksMeter is provided at http://rllinstruments.com . Some backgraound and characteristics are to be found at http://seismicnet.com/Volksmeter/State-of-the-art_Digital_Seismograph.pdf
[8] The spec sheet for the AD7745 is at http://www.analog.com/en/prod/0,2877,AD7745,00.html
[9] R. Peters, ``A New Tool for Seismology-the Cumulative Spectral Power'', online at http://physics.mercer.edu/hpage/CSP/cumulative.html

File translated from T_EX by T_TH, version 1.95.
On 11 Aug 2007, 15:11.