1  Introduction

The sensitivity of a simple harmonic oscillator (SHO) to external acceleration (forcing) is proportional to the square of the natural period of the oscillator. High sensitivity from a vertically oriented, simple spring/mass system, would require an inordinately long (weak) spring. Not only would such a seismometer be unwieldy; but it would be afflicted with unnecessary noises. 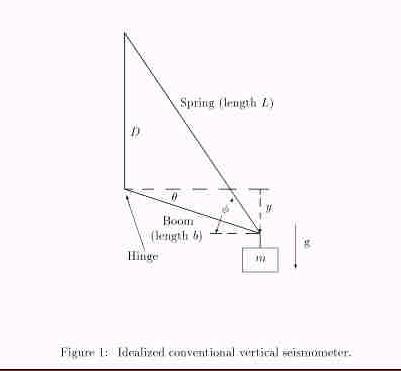A common solution to this problem is to incline the spring away from vertical, such as in the Press-Ewing vertical seismometer, illustrated in Fig. 1.

Assuming no damping, no drive, and a weightless (rigid) boom and spring; the equation of motion is given by

where g is the magnitude of the gravitational field, k is the spring constant; the unstretched length of the spring is  L₀ , and the angles are as indicated.

In analyzing this system, it is convenient to employ the law of sines.

An equilibrium relation is found by setting [(q)\ddot] ® 0 , in Eq. (1), from which

where  L_e  is the length of the spring at equilibrium (when  y  =  0 ).

For small motions,  ¹/_L  »  [1/( L_e)] ( 1 -[(DL)/( L_e)] )  with  DL  »  y sin f_e . Thus the equation of motion for the system becomes

Since the parenthetic expression multiplying  y  involves the angular frequency of the simple harmonic motion (w₀² ), it is seen that the period of the motion is inversely proportional to  sin f_e . In principle, one could therefore extend the period,  T , without limit as  D® 0  (since  sin f_e  =  D/L_e ). It is clear from the figure, however, that this tends toward an equilibrium which at best is approximately neutral; and which at worst is unstable. In practice, it is very difficult to work with such a system having a period  T  >  30 s  because of material limitations associated with anelasticity.

An ordinary spring does not perform well in the Fig. 1 configuration. Many conventional seismometers have thus utilized the so-called ``zero-length" spring, invented by La Coste and patented in the 1930's. Although designed originally for use in gravimeters (La Coste Romberg types being very popular), the spring has found widespread use in vertical seismometers of the conventional (non force-balance) type.

From Eq. (4), it is seen that  T  can be lengthened by letting  L₀ ® 0 , even though  f_e  =  constant . Working with  L₀  near zero and  f_e  » p/4  has been a popular combination, widely used in the World Wide Standard Network.

What is meant by the term, ``zero-length"? If there were no constraint due to the finite wire diameter of such a helical spring, it would have zero length in the unstretched condition. To achieve this, a twist is introduced into the wire as it is coiled, in the manufacturing process. This works because a coiled spring ``unwinds" as it is stretched. An appreciation for this phenomenon can be realized by noting that the dominant modulus, insofar as the spring constant is determined, is that of the shear modulus.

To appreciate the value of the zero-length spring from a stability standpoint, consider the equation of motion, Eq. 4. Although this equation implies infinite period for L₀  =  0, it was derived under the assumption of very small motion. A treatment of the problem to allow larger vertical motion of m would show that it's impossible to have the effective spring constant k_eff  =  kL₀ sin²f_e/L_e to be identically zero. Nevertheless, k_eff is small because of L₀ being small, even though sin f_e is large (near p/4). For a non-zero length spring, the only way k_eff can be made small is by forcing sinf_e to a small value. In so doing, one moves in the direction of instability, as is obvious from figure 1. Small changes in the spring characteristic, due to thermal change or anelastic change-give rise to large changes in y.

2  Modern Seismometers

The modern force-balance seismometer does not utilize a zero-length spring. It relies on electronic feedback to ``soften'' a strong spring. Thus k<sub>eff</sub> is made small by proper phase and amplitude feedback to a transducer whose adjustable upward force augments typically a ``hard'' leaf spring. It is tempting to believe that the force-balance technique has somehow eliminated the problems of anelasticity that plague the non zero-length spring of a conventional type. First, let us note, that it is not possible to correct a poor mechanical design by electronics means. In other words, problems of anelasticity (small amplitude, long period nonlinearity) must still be present in such an instrument-they've just been camouflaged.

It is the author's belief that the use of a zero-length spring as the basis for a force-balance instrument would be superior to the systems presently in use; i.e., build a vertical seismometer (large mass unit) employing the same principle as those of the modern LaCoste Romberg gravimeter (which the author understands to use a small zero-length quartz spring and force-balancing by means of a capacitive transducer). Of course the large force of feedback must be accomplished by means of magnetic force, for the large mass. It should be noted that the magnetic force is not devoid of anelastic (nonlinear) problems, through the Barkhausen effect.